A partir de um ponto, observa-se o topo de um prédio sob um ângulo de \( 30^\circ \).
Caminhando 24 m em direção ao prédio, atinge-se outro ponto, de onde se vê o topo do prédio segundo um ângulo de \( 60^\circ \).
Desprezando a altura do observador, calcule, em metro, a altura do prédio.
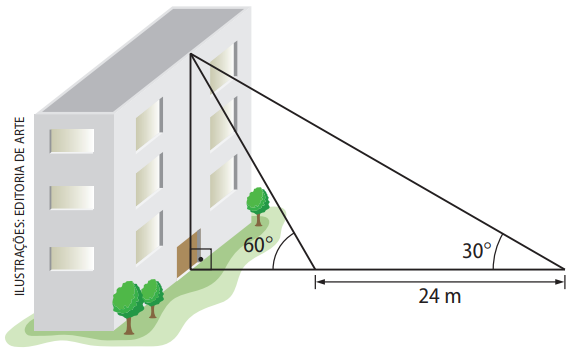
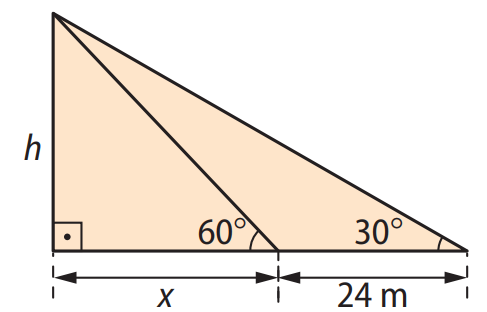
Seja \( h \) a altura do prédio e \( x \) a distância do ponto mais próximo ao prédio. Temos os seguintes sistemas de equações:
Substituindo \( x \) da equação (I) na (II):
Portanto, a altura do prédio é \( 12 \sqrt{3} \, \text{m} \).
📖 Leia Também
Descubra tudo sobre ângulos de 30°, 45° e 60° e aprenda as principais razões trigonométricas de forma simples e objetiva.
📚 Coleção de Livros Indispensáveis
Volume 3: Trigonometria
Domine a trigonometria com explicações claras, exemplos práticos e conteúdo completo para estudo.
🔗 Acesse na AmazonVolume 9: Geometria Plana
Estude os conceitos de geometria plana com uma abordagem didática e repleta de exemplos.
🔗 Acesse na AmazonVolume 10: Geometria Espacial
Aprofunde-se nos estudos da geometria espacial com conteúdos explicativos e exercícios práticos.
🔗 Acesse na Amazon












