Fórmula do Volume da Esfera
A esfera é um dos principais corpos redondos: o conjunto dos pontos do espaço à mesma distância do seu centro. Essa distância é o raio \(r\). Para propriedades completas e área da superfície, consulte o artigo Esfera.
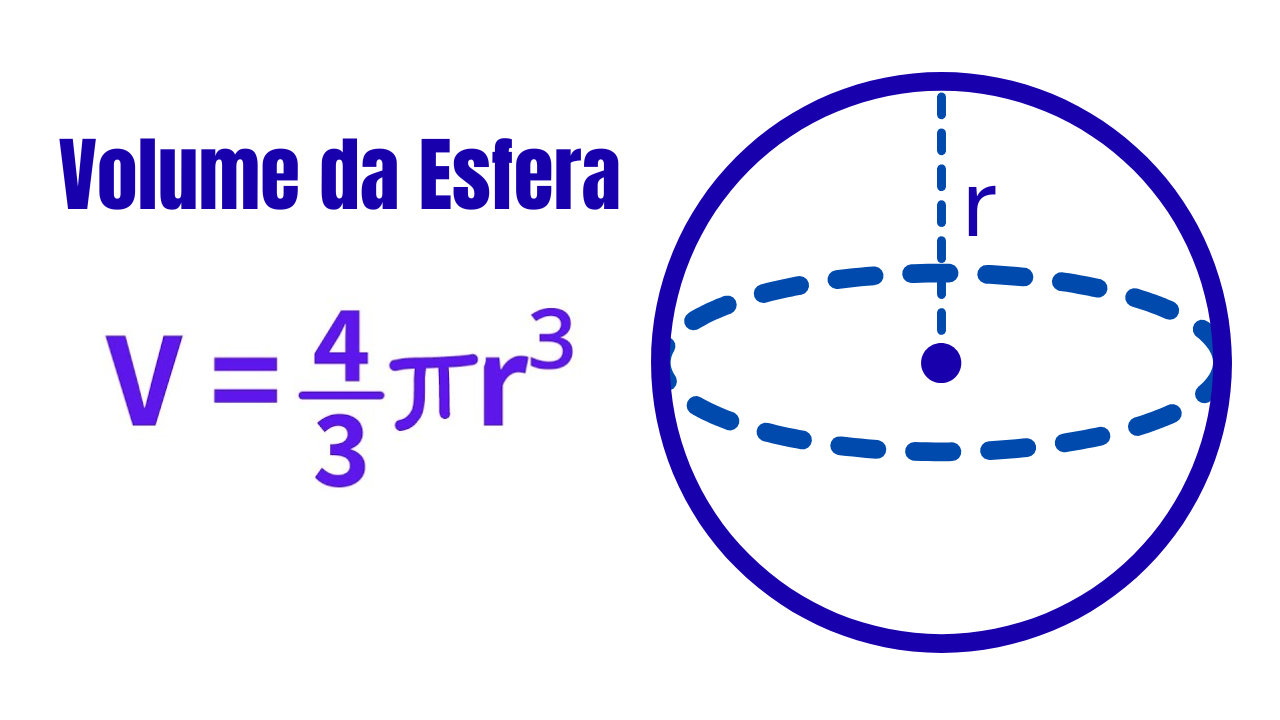
Fórmula principal
- \(V\): volume (em unidades cúbicas: cm³, m³, …);
- \(\pi\): constante aproximadamente \(3{,}14159\);
- \(r\): raio da esfera.
Por que essa fórmula? (intuição rápida)
Há várias demonstrações. Uma delas usa o Princípio de Cavalieri: ao comparar, para cada altura, as áreas de cortes de um cilindro com cone interno com as da esfera, mostra-se que os volumes são equivalentes, concluindo \(V_{\text{esfera}}=\tfrac{2}{3}V_{\text{cilindro}}\). Como o cilindro inscrito tem raio \(r\) e altura \(2r\), \(V_{\text{cilindro}}=\pi r^{2}\cdot 2r=2\pi r^{3}\). Logo, \(V=\tfrac{2}{3}\cdot 2\pi r^{3}=\tfrac{4}{3}\pi r^{3}\).
Variações úteis da fórmula
- Em função do diâmetro \(d=2r\):
\( \displaystyle V=\frac{\pi}{6}\,d^{3} \)
- Isolando o raio a partir do volume:
\( \displaystyle r=\sqrt[3]{\frac{3V}{4\pi}} \)
- Escala: se o raio é multiplicado por \(k\), o volume multiplica por \(k^{3}\).
Unidades e conversões
Use sempre unidades cúbicas. Para aplicações práticas, lembre que \(1\,\text{m}^{3}=1000\,\text{L}\).
Exemplos resolvidos
Exemplo 1. Calcule o volume de uma esfera de raio \(r=5\text{ cm}\).
Exemplo 2. Uma esfera tem volume \(904{,}32\ \text{cm}^{3}\). Encontre o raio.
Compare com outros sólidos
- Volume do cubo
- Volume do paralelepípedo
- Mais prática: Exercício Esfera
Erros comuns
- Usar o diâmetro no lugar do raio sem dividir por 2.
- Esquecer a potência cúbica \(r^{3}\).
- Responder em unidades quadradas em vez de cúbicas.
Exercícios (múltipla escolha)
1) Uma bolinha de gude tem diâmetro \(1{,}6\ \text{cm}\). O volume aproximado da bolinha é:
- A) \(1{,}37\ \text{cm}^{3}\)
- B) \(2{,}14\ \text{cm}^{3}\)
- C) \(3{,}00\ \text{cm}^{3}\)
- D) \(4{,}19\ \text{cm}^{3}\)
Ver solução
Resposta: B.
2) O volume de uma esfera é \(288\pi\ \text{cm}^{3}\). Qual é o raio?
- A) \(4\ \text{cm}\)
- B) \(5\ \text{cm}\)
- C) \(6\ \text{cm}\)
- D) \(8\ \text{cm}\)
Ver solução
Resposta: C.
3) Uma bola oficial tem raio \(12\ \text{cm}\). O volume exato é:
- A) \(1728\pi\ \text{cm}^{3}\)
- B) \(2304\pi\ \text{cm}^{3}\)
- C) \(2592\pi\ \text{cm}^{3}\)
- D) \(3072\pi\ \text{cm}^{3}\)
Ver solução
Resposta: B.
4) Um reservatório esférico tem raio \(1{,}2\ \text{m}\). Qual é a capacidade em litros (aprox.)?
- A) \(7\,240\ \text{L}\)
- B) \(8\,680\ \text{L}\)
- C) \(9\,050\ \text{L}\)
- D) \(7\,240\ \text{mL}\)
Ver solução
Resposta: A.
5) Uma esfera maciça de raio \(r\) é alongada para outra com raio \(2r\). O volume é multiplicado por:
- A) 2
- B) 3
- C) 4
- D) 8
Ver solução
Escala de volumes: \(V\propto r^{3}\).
Resposta: D.
Quer mais prática? Veja: Exercício Esfera. E compare com outros sólidos: Cubo e Paralelepípedo.






















