Função Afim: Definição, Exemplos e Exercícios Resolvidos

A função afim, também chamada de função do 1º grau, é uma das mais importantes da matemática básica. Ela aparece com frequência em questões do ENEM, em vestibulares e em provas de concursos públicos. Estudar esse tema é essencial para quem busca uma preparação sólida em matemática.
O que é Função Afim?
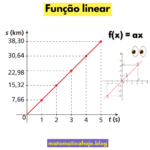
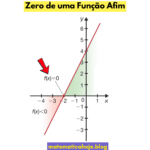
A função afim é toda função que pode ser escrita da forma:
onde:
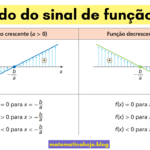
- a é o coeficiente angular (indica a inclinação da reta);
- b é o coeficiente linear (indica onde a reta intercepta o eixo y);
- x é a variável independente.
Exemplo Prático
Considere a função:
Ela pode representar, por exemplo, o valor de um estacionamento, em que:
- O cliente paga uma taxa fixa de R$ 3,00.
- Além disso, paga R$ 0,80 por cada minuto estacionado.
Veja na tabela abaixo como a função é aplicada:
Exemplo Resolvido
Exemplo: Qual será o valor pago por 10 minutos de estacionamento?
Ver solução passo a passo
\( f(x) = 0,80 \cdot x + 3 \)
\( f(10) = 0,80 \cdot 10 + 3 \)
\( f(10) = 8 + 3 \)
\( f(10) = 11 \)
Resposta: O cliente pagará R$ 11,00.
Exercícios Resolvidos
Questão 1: Uma corrida de táxi é cobrada segundo a função \( f(x) = 5x + 10 \), onde x representa os quilômetros percorridos. Qual o valor da corrida para 12 km?
Ver solução
\( f(12) = 5 \cdot 12 + 10 \)
\( f(12) = 60 + 10 \)
\( f(12) = 70 \)
Resposta: R$ 70,00.
Questão 2: Uma empresa de telefonia cobra uma taxa fixa de R$ 20,00 mais R$ 0,50 por minuto de ligação. Escreva a função que representa o valor total a ser pago e calcule o preço de uma ligação de 30 minutos.
Ver solução
Função: \( f(x) = 0,50x + 20 \)
\( f(30) = 0,50 \cdot 30 + 20 \)
\( f(30) = 15 + 20 \)
\( f(30) = 35 \)
Resposta: R$ 35,00.
Questão 3: Em uma gráfica, o custo de imprimir cartazes é dado por \( f(x) = 2x + 50 \), onde x é o número de cartazes. Quanto será o custo para imprimir 100 cartazes?
Ver solução
\( f(100) = 2 \cdot 100 + 50 \)
\( f(100) = 200 + 50 \)
\( f(100) = 250 \)
Resposta: R$ 250,00.
Conclusão
A função afim está presente em diversas situações cotidianas, como tarifas de transporte, contas de telefone e taxas de serviços. Dominar esse conteúdo é fundamental para quem deseja se preparar bem para provas e concursos.
👉 Veja também: