Função Afim Crescente e Decrescente
Neste guia você aprende a identificar rapidamente se uma função afim \(f(x)=ax+b\) é crescente ou decrescente, interpretando o coeficiente angular e a razão \(\Delta y/\Delta x\). Ao final, resolva exercícios com gabarito. Quer revisar toda a teoria? Veja também: Construção do gráfico da função afim Taxa de variação da função afim Zero da função afim Interseção de retas Função linear (b=0) Função constante (a=0)
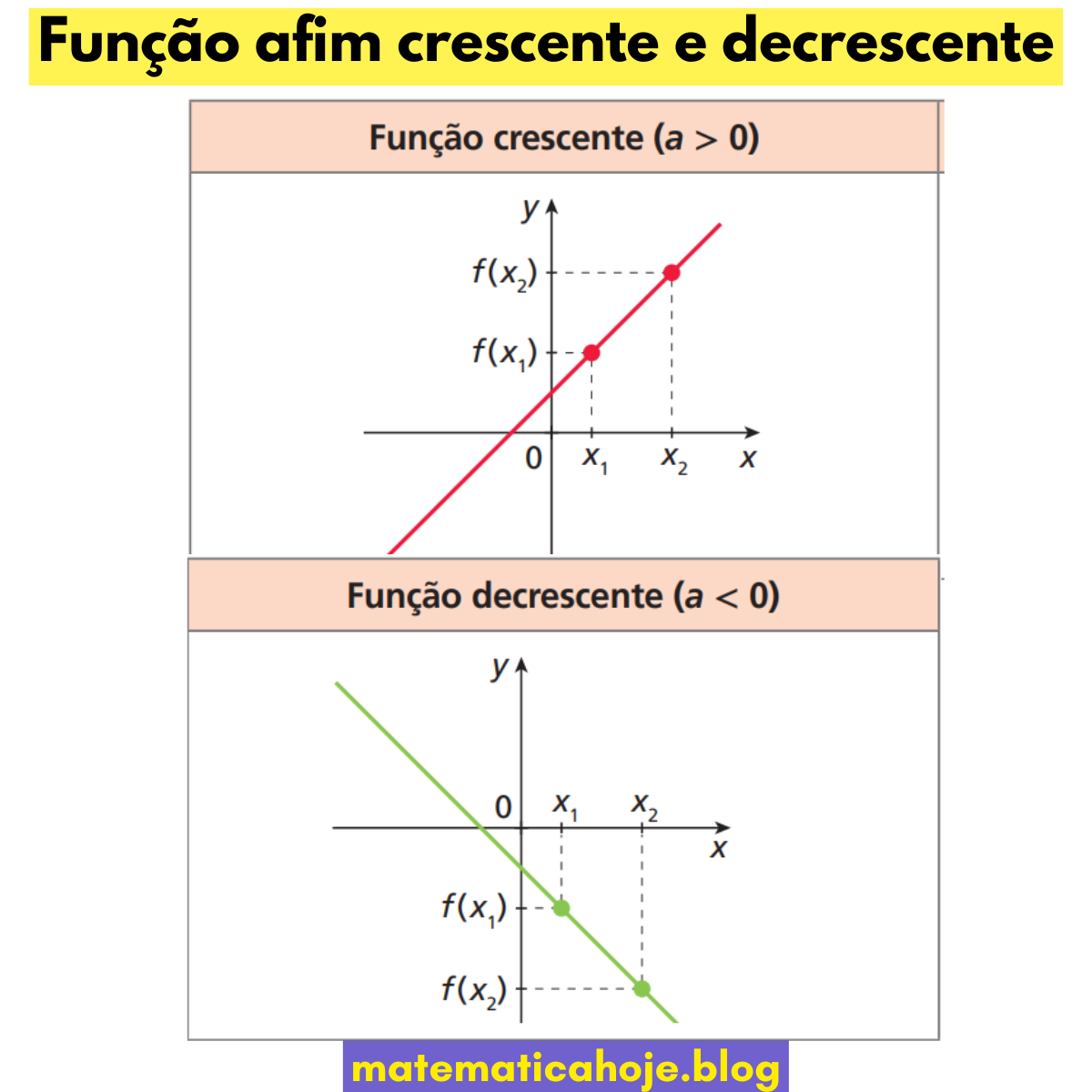
Critério geral
No gráfico, o sinal de \(a\) é a própria inclinação \(\dfrac{\Delta y}{\Delta x}\): sobe se \(a>0\) e desce se \(a<0\). A taxa de variação é explicada em detalhes aqui: Δy/Δx da função afim.
Como decidir a partir de dados
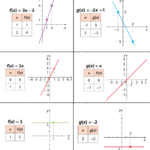
- Pela lei \(f(x)=ax+b\): olhe o sinal de \(a\).
- Por dois pontos \(P(x_1,y_1)\), \(Q(x_2,y_2)\): calcule \(a=\dfrac{y_2-y_1}{x_2-x_1}\).
- No gráfico: compare dois pontos quaisquer — se a reta sobe da esquerda para a direita, é crescente.
📘 Reforço de estudo
Revise os principais tópicos de funções com o eBook Fórmulas Matemática (super prático para provas e listas).
Baixar eBook de FórmulasExemplos resolvidos
Exemplo 1 — Pela lei. Classifique \(f(x)=-3x+2\). Encontre ainda o zero e descreva a variação de \(f\) quando \(x\) aumenta 5 unidades.
Ver solução
\(a=-3<0\) ⇒ decrescente. Zero: \(x_0=-\dfrac{b}{a}=-\dfrac{2}{-3}=\dfrac{2}{3}\) (veja zero da função).
Se \(\Delta x=5\), então \(\Delta f=a\Delta x=-3\cdot 5=-15\) ⇒ o valor diminui 15 unidades.
Exemplo 2 — A partir de dois pontos. Uma reta passa por \(A(1,4)\) e \(B(5,16)\). Classifique e ache \(f(x)\).
Ver solução
\(a=\dfrac{16-4}{5-1}=\dfrac{12}{4}=3>0\) ⇒ crescente. Usando \(A\): \(4=3\cdot1+b\Rightarrow b=1\). Logo \(f(x)=3x+1\).
Exemplo 3 — Leitura no gráfico. A reta sobe 2 unidades em \(y\) a cada 1 em \(x\). Classifique e escreva uma possível lei.
Ver solução
Inclinação \(a=2>0\) ⇒ crescente. Uma lei possível que passa pela origem é \(f(x)=2x\) (veja função linear).
Exercícios (com solução no abre/fecha)
1) Para \(g(x)=0{,}8x+3\): classifique e determine a variação de \(g\) quando \(x\) aumenta de 2 unidades.
Ver solução
\(a=0{,}8>0\) ⇒ crescente. \(\Delta g=a\Delta x=0{,}8\cdot 2=1{,}6\).
2) A função \(h(x)=-1{,}5x+6\) é crescente ou decrescente? Calcule \(h(0)\), \(h(2)\) e o zero.
Ver solução
Decrescente (\(a=-1{,}5\)). \(h(0)=6\), \(h(2)=3\). Zero: \(x_0=-\dfrac{6}{-1{,}5}=4\).
3) Uma reta contém \(P(-1,2)\) e \(Q(3,-6)\). Classifique e ache \(a\) e \(b\).
Ver solução
\(a=\dfrac{-6-2}{3-(-1)}=\dfrac{-8}{4}=-2\) ⇒ decrescente.
Usando \(P\): \(2=-2\cdot(-1)+b \Rightarrow b=0\). \(f(x)=-2x\) (linear).
4) Para \(p(x)=ax-4\), determine as condições para ser: a) crescente; b) decrescente; c) constante.
Ver solução
a) \(a>0\). b) \(a<0\). c) \(a=0\) ⇒ \(p(x)=-4\) (veja função constante).
5) Verifique se a tabela é compatível com uma função afim e classifique:
\(x:\ 0,\ 4,\ 8\) e \(f(x):\ 7,\ -5,\ -17\).
Ver solução
Entre 0 e 4: \(\dfrac{-5-7}{4-0}=-3\). Entre 4 e 8: \(\dfrac{-17-(-5)}{8-4}=-3\). Taxa constante ⇒ é afim com \(a=-3<0\) (decrescente). Usando \(x=0\): \(b=7\) ⇒ \(f(x)=-3x+7\).
Leia também (função afim — série completa)
- Como construir o gráfico da função afim
- Zero de uma função afim
- Taxa de variação da função afim
- Interseção de retas
- Função linear • Função constante