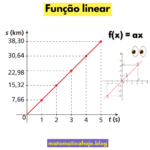
Função Constante
Chamamos de função constante toda função que associa o mesmo valor a qualquer entrada. É um caso particular da função afim com coeficiente angular nulo (\(a=0\)). Tema simples e muito cobrado em ENEM, vestibulares e concursos.

Definição
isto é, \( f(x)=0\cdot x + b \).
Gráfico
O gráfico é uma reta horizontal que corta o eixo \(y\) no ponto \((0,b)\). Não há inclinação porque o coeficiente angular é \(a=0\).
Propriedades principais
- Domínio: em geral, \(\mathbb{R}\) (ou conforme o contexto).
- Imagem (contradomínio efetivo): \(\{b\}\) (apenas um valor).
- Zeros: se \(b=0\), todo \(x\) é zero (função nula). Se \(b\neq 0\), não possui zeros.
- Monotonia: é não-crescente e não-decrescente ao mesmo tempo (é constante).
- Paridade: é par e ímpar apenas quando \(b=0\).
- Derivada: \(f'(x)=0\). Integral: \(\displaystyle \int f(x)\,dx=b\,x+C\).
📘 Precisa das fórmulas sempre à mão?
Baixe o eBook Fórmulas Matemática com resumos de funções, geometria e estatística. Ótimo para revisar antes da prova.
Baixar eBook de FórmulasRelação com a Função Afim
A função afim tem a forma \(f(x)=ax+b\). Quando \(a=0\), obtemos \(f(x)=b\) (função constante). Assim, é um caso particular da função do 1º grau.
Exemplos resolvidos
Exemplo 1 — Interceptos e zeros. Para \(f(x)=5\), determine o ponto de interseção com os eixos e os zeros da função.
Ver solução
Interseção com \(y\): \((0,5)\). Interseção com \(x\): não existe (a reta é horizontal acima do eixo).
Zeros: como \(b=5\neq 0\), não há zeros.
Exemplo 2 — Contexto físico (velocidade constante). Seja \(v(t)=2\,\text{m/s}\) para todo \(t\ge 0\) e posição inicial \(s(0)=10\,\text{m}\). Encontre \(s(t)\).
Ver solução
\(s'(t)=v(t)=2\). Integrando: \(s(t)=2t+C\). Como \(s(0)=10\), temos \(C=10\).
Logo: \(s(t)=2t+10\) (função afim resultante).
Exemplo 3 — Encontro com uma reta oblíqua. A constante \(g(x)=3\) intercepta \(h(x)=2x-1\) em qual \(x\)?
Ver solução
Resolva \(3=2x-1 \Rightarrow 2x=4 \Rightarrow x=2\). Ponto de interseção: \((2,3)\).
Exercícios (com soluções no abre/fecha)
1) Dada \(f(x)=-3\): indique domínio, imagem, interseções com os eixos, zeros e esboce o gráfico.
Ver solução
Domínio: \(\mathbb{R}\). Imagem: \(\{-3\}\).
Interseção com \(y\): \((0,-3)\). Com \(x\): não existe.
Zeros: inexistentes (\(b\neq 0\)). Gráfico: reta horizontal em \(y=-3\).
2) Considere \(c(x)=k\) com \(k\neq 0\). Essa função é injetiva? É sobrejetiva em \(\mathbb{R}\)? Justifique.
Ver solução
Não é injetiva: \(c(x_1)=c(x_2)=k\) para quaisquer \(x_1,x_2\).
Não é sobrejetiva em \(\mathbb{R}\): a imagem é \(\{k\}\), não todo \(\mathbb{R}\).
3) Uma plataforma cobra mensalidade fixa de R$ 49,90, independentemente do uso. Modele o custo mensal \(C(m)\) em função do número de horas \(m\) e diga o gráfico.
Ver solução
\(C(m)=49{,}90\) (função constante). Gráfico: reta horizontal no nível \(49{,}90\) para \(m\ge 0\).
4) Para qual valor de \(b\) a função constante \(f(x)=b\) possui infinitos zeros?
Ver solução
Para \(b=0\). Nesse caso, \(f(x)=0\) para todo \(x\) e todo ponto do eixo \(x\) é raiz.
5) Dada \(f(x)=b\) e \(g(x)=ax+b\) com \(a\neq 0\), encontre a abscissa do ponto de interseção.
Ver solução
Iguale: \(b=ax+b \Rightarrow ax=0 \Rightarrow x=0\). A interseção ocorre em \(x=0\) e \(y=b\).
Continue seus estudos
- Funções Matemáticas (visão geral)
- Função Quadrática
- Banco de Questões de Matemática • ENEM Matemática