Função Cosseno
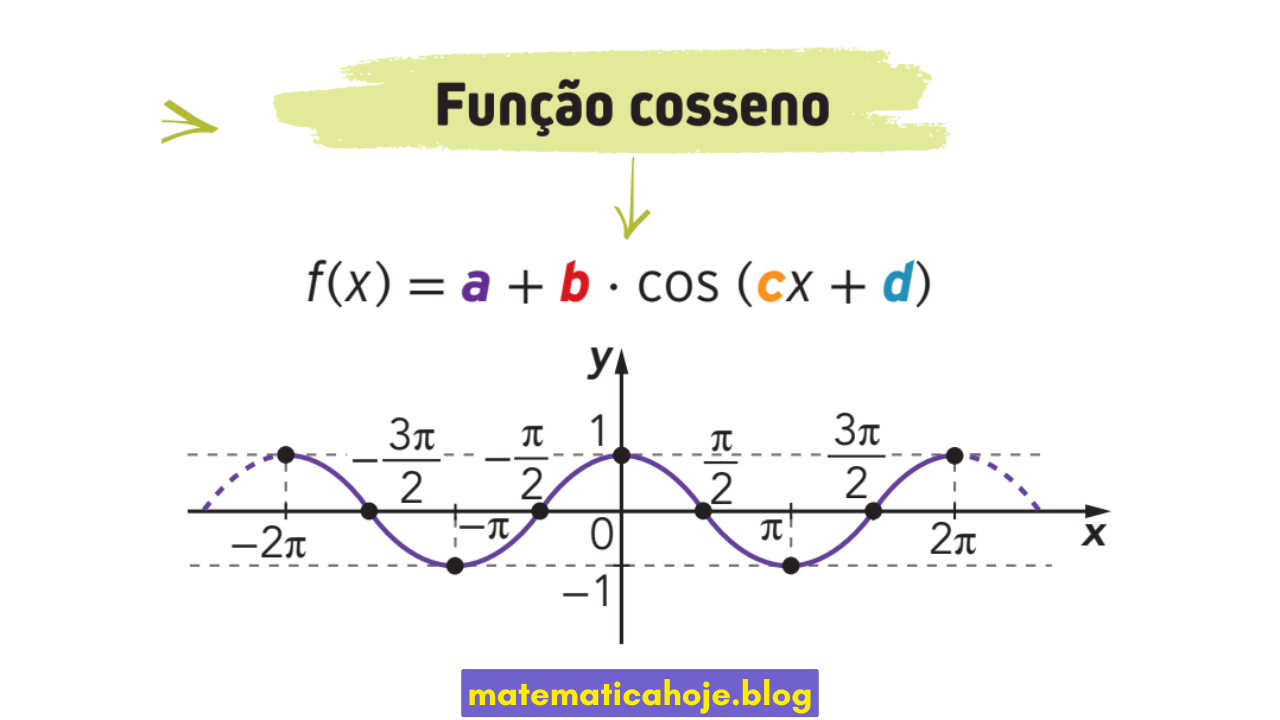
A função cosseno é uma das funções trigonométricas mais utilizadas em Matemática. Assim como a função seno, ela modela fenômenos periódicos, mas com uma diferença fundamental: seu valor máximo ocorre em \(x=0\). Isso a torna muito útil em situações que começam com valor máximo ou mínimo.
\( f(x) = a + b \cdot \cos(cx + d) \)
Componentes da Função
- a: deslocamento vertical (translada o gráfico para cima ou para baixo).
- b: amplitude (determina a altura máxima e mínima do gráfico).
- c: frequência angular (define o número de ciclos em \(2\pi\)).
- d: fase (desloca o gráfico para esquerda ou direita).
Propriedades da Função Cosseno
- Domínio: todos os números reais (\(\mathbb{R}\)).
- Imagem: \([-1,1]\) na forma básica.
- Período: \(2\pi/c\).
- Função par: \(\cos(-x)=\cos(x)\).
Exemplo Resolvido
Exemplo: Determine a amplitude e o período da função \(f(x)=2\cos(3x)\).
Solução:
• Amplitude = 2.
• Período = \(\dfrac{2\pi}{3}\).
Lista de Exercícios
1) A imagem da função \(f(x)=-4\cos(x)\) é:
A) \([-1,1]\)
B) \([-2,2]\)
C) \([-3,3]\)
D) \([-4,4]\)
Ver solução
A amplitude é 4. Logo, a imagem é \([-4,4]\). Resposta: D.
2) O período da função \(f(x)=\cos(5x)\) é:
A) \(2\pi\)
B) \(\pi\)
C) \(\dfrac{2\pi}{5}\)
D) \(\dfrac{\pi}{5}\)
Ver solução
O período é \(\dfrac{2\pi}{c}=\dfrac{2\pi}{5}\). Resposta: C.
3) Para a função \(f(x)=1+\cos(x)\), qual é a imagem?
A) \([-1,1]\)
B) \([0,2]\)
C) \([1,3]\)
D) \([-2,2]\)
Ver solução
A imagem básica é \([-1,1]\). Com o deslocamento +1, passa a ser \([0,2]\). Resposta: B.






















