Função do Segundo Grau – Concurso Correios 2008 – Banca CONSULPLAN
Qual é a lei da função representada pelo gráfico abaixo?
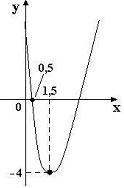
A) y = x² – 2,5x + 5
B) y = í 4x² – 2x + 10
C) y = 4x² – 12x + 5
D) y = 2x² – 12x + 5
E) y = x² – 0,5x + 5
Ver Solução
Vamos resolver o problema usando as informações fornecidas e montar um sistema de equações para encontrar os coeficientes (a), (b) e (c).
Passo 1: Fórmula geral da função quadrática
Sabemos que a equação da função quadrática tem a forma:
y = ax2 + bx + c
Passo 2: Usando os pontos fornecidos
Temos as seguintes informações:
- O vértice está no ponto (1,5; -4),
- O ponto (0,5; 0) também pertence à parábola.
Além disso, o valor de yv = -4 (valor do vértice).
Passo 3: Montando o sistema de equações
- Primeira equação (vértice (1,5, -4) ):
Substituímos x = 1,5 e y = -4 na equação geral:
-4 = a(1,5)2 + b(1,5) + c
-4 = a(2,25) + 1,5b + c
2,25a + 1,5b + c = -4
- Segunda equação ponto (0,5; 0):
Substituímos (x = 0,5) e (y = 0) na equação geral:
0 = a(0,5)2 + b(0,5) + c
0 = a(0,25) + 0,5b + c
0,25a + 0,5b + c = 0
- Terceira Equação: Utilizando xv = 1,5, temos:
xv = -b/2a
1,5= -b/2a
1,5 x 2a= -b
b = -3a
Passo 4: Resolvem o sistema
Agora, temos um sistema com três equações:
Vamos resolver o sistema de equações passo a passo.
Sistema de Equações
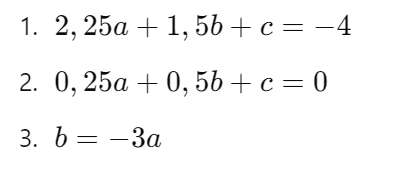
Passo 1: Substituir ( b ) na Equação 1 e 2
Usando a Equação 3 (b = -3a), substituímos ( b ) nas equações 1 e 2.
Substituindo na Equação 2:
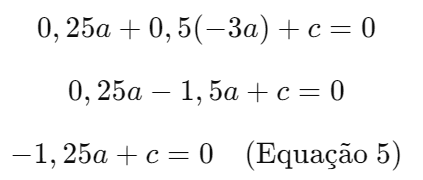
Passo 2: Resolver o Sistema com as Equações 4 e 5
Agora temos um sistema com duas equações e duas incógnitas:
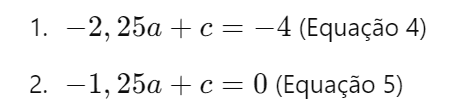
Vamos subtrair a Equação 5 da Equação 4 para eliminar ( c ).
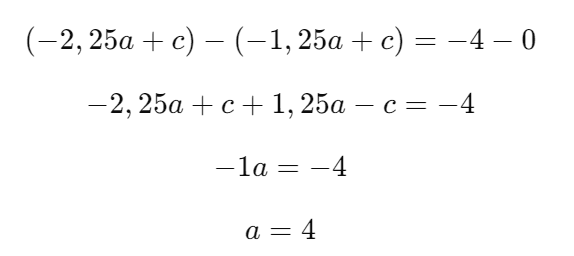
Passo 3: Encontrar ( c )
Substituímos ( a = 4 ) em qualquer uma das Equações 4 ou 5 para encontrar ( c ).
Usando a Equação 5:
Passo 4: Encontrar ( b )
Agora, usamos a Equação 3 para encontrar ( b ).
Solução Final
Os valores encontrados são:
- ( a = 4 )
- ( b = -12 )
- ( c = 5 )
Esses são os valores das variáveis que satisfazem todas as equações do sistema.
Logo y = 4x2 – 12 + 5
