Função quadrática: gráfico, Δ (delta) e concavidade — exemplos resolvidos e exercícios
Veja como a concavidade (sinal de a) e o discriminante (Δ = b² − 4ac) determinam o desenho da parábola. No fim, resolva exercícios com as contas em coluna.
Mapas mentais de Matemática
Resumos visuais para revisar função quadrática e todo o conteúdo do ensino médio.
Ver mapasENEM Matemática
Trilhas de estudo, questões comentadas e simulados com foco no ENEM.
Preparar o ENEMO que observar no gráfico
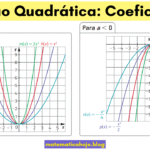
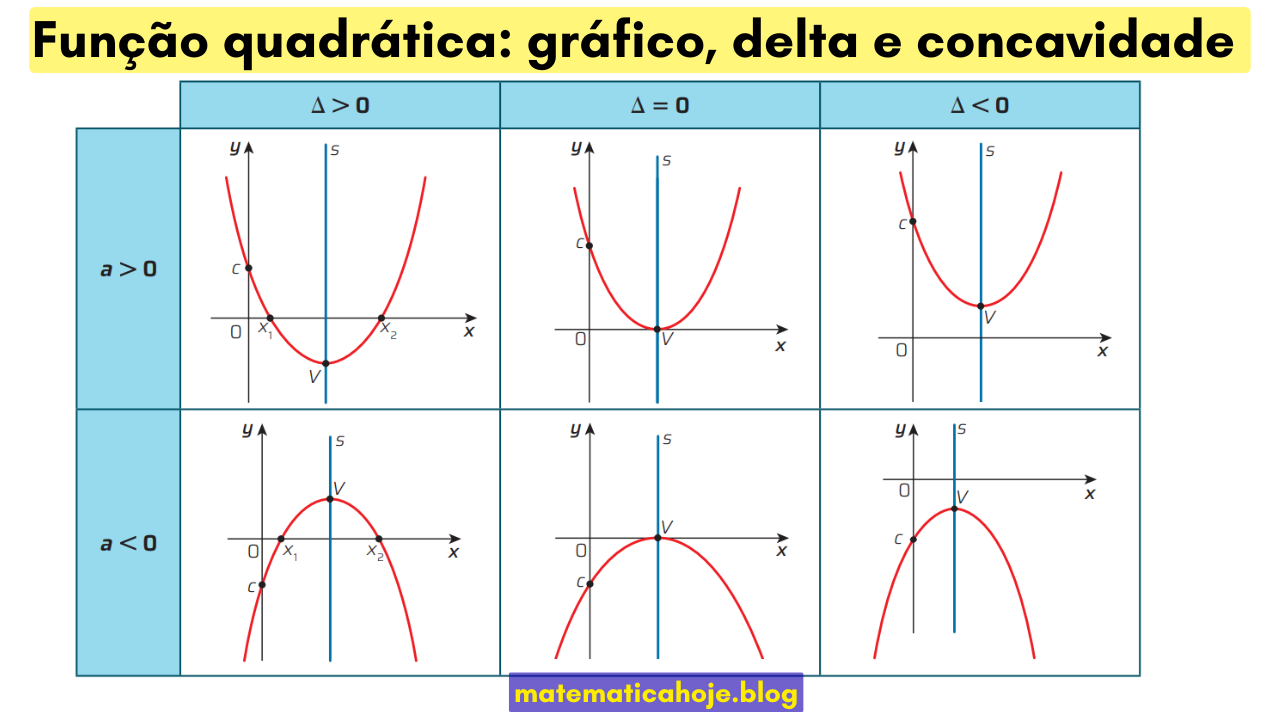
Concavidade Se \(a>0\), a parábola é côncava para cima (abre “para cima”); se \(a<0\), é côncava para baixo.
Raízes Dependem de \(\Delta=b^2-4ac\): se \(\Delta>0\) há duas raízes reais; se \(\Delta=0\) há uma raiz real dupla; se \(\Delta<0\), não há raízes reais.
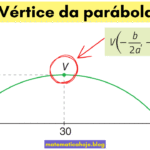
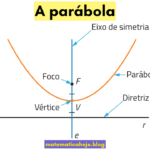
Vértice Coordenadas \(V(x_v,y_v)\) com \(x_v=-\dfrac{b}{2a}\) e \(y_v=-\dfrac{\Delta}{4a}\). É o ponto de máximo (se \(a<0\)) ou de mínimo (se \(a>0\)).
Exemplos resolvidos (contas em coluna)
Exemplo 1 — Para \(f(x)=2x^2-4x+1\), determine \(\Delta\), o vértice \(V(x_v,y_v)\), as raízes e a concavidade. Apresente as contas em coluna.
Concavidade: \(a=2 > 0\) (para cima).
Delta:
\[\Delta=b^2-4ac\]
\[= (-4)^2-4\cdot 2\cdot 1\]
\[= 16-8\]
\[= 8\]
Vértice:
\[x_v=-\frac{b}{2a}\]
\[= -\frac{-4}{2\cdot 2}\]
\[= \frac{4}{4}\]
\[= 1\]
\[y_v=-\frac{\Delta}{4a}\]
\[= -\frac{8}{4\cdot 2}\]
\[= -\frac{8}{8}\]
\[= -1\]
Raízes:
\[x=\frac{-b\pm\sqrt{\Delta}}{2a}\]
\[= \frac{-(-4)\pm\sqrt{8}}{2\cdot 2}\]
\[= \frac{4\pm 2\sqrt{2}}{4}\]
\[= \frac{2\pm \sqrt{2}}{2}\]
Conclusão: parábola para cima, \(V(1,-1)\) e duas raízes reais distintas.
Baixar o eBook • Fórmulas de Matemática
Exemplo 2 — Para \(g(x)=-3x^2+6x-5\), determine \(\Delta\), o vértice \(V(x_v,y_v)\), verifique a existência de raízes e informe a concavidade.
Concavidade: \(a=-3 < 0\) (para baixo).
Delta:
\[\Delta=b^2-4ac\]
\[= 6^2-4\cdot(-3)\cdot(-5)\]
\[= 36-60\]
\[= -24\]
Vértice:
\[x_v=-\frac{b}{2a}\]
\[= -\frac{6}{2\cdot(-3)}\]
\[= -\frac{6}{-6}\]
\[= 1\]
\[y_v=-\frac{\Delta}{4a}\]
\[= -\frac{-24}{4\cdot(-3)}\]
\[= \frac{24}{-12}\]
\[= -2\]
Como \(\Delta<0\), não existem raízes reais. Conclusão: parábola para baixo, \(V(1,-2)\), sem interceptar o eixo \(x\).
Exercícios propostos
Exercício 1 (aberto) — Para \(f(x)=x^2-6x+8\), calcule \(\Delta\), o vértice \(V\), as raízes e esboce o gráfico.
Ver solução
\[\Delta=b^2-4ac\]
\[= (-6)^2-4\cdot 1\cdot 8\]
\[= 36-32\]
\[= 4\]
\[x_v=-\frac{b}{2a}=-\frac{-6}{2\cdot 1}=\frac{6}{2}=3\]
\[y_v=-\frac{\Delta}{4a}=-\frac{4}{4\cdot 1}=-1\]
\[x=\frac{-b\pm\sqrt{\Delta}}{2a} =\frac{-(-6)\pm 2}{2} =\frac{6\pm 2}{2} = \{2,4\}\]
Exercício 2 (aberto) — Para \(g(x)=2x^2+4x+5\), classifique \(\Delta\), encontre \(V\) e diga se há raízes reais.
Ver solução
\[\Delta=4^2-4\cdot 2\cdot 5=16-40=-24\]
\[x_v=-\frac{b}{2a}=-\frac{4}{4}=-1\]
\[y_v=-\frac{\Delta}{4a}=-\frac{-24}{8}=3\]
\(\Delta<0\Rightarrow\) sem raízes reais.
Exercício 3 (múltipla escolha) — Para \(h(x)=-x^2-2x+3\), assinale a alternativa correta.
- Concavidade para cima e duas raízes.
- Concavidade para baixo e duas raízes.
- Concavidade para baixo e nenhuma raiz.
- Concavidade para cima e uma raiz dupla.
Gabarito e solução
\[a=-1 \Rightarrow \text{concavidade para baixo}\]
\[\Delta=(-2)^2-4\cdot(-1)\cdot 3=4+12=16\]
\[\Delta>0 \Rightarrow \text{duas raízes}\]
Resposta: (b).
Exercício 4 (múltipla escolha) — A função \(p(x)=x^2+4x+4\) possui:
- Duas raízes reais e distintas.
- Uma raiz real dupla.
- Nenhuma raiz real.
- Não é possível concluir.
Gabarito e solução
\[\Delta=4^2-4\cdot 1\cdot 4=16-16=0\]
\[\Delta=0 \Rightarrow \text{raiz real dupla}\]
Resposta: (b).
Materiais recomendados
Complete seu kit com o pacote de mapas mentais e o eBook de fórmulas.
Para estudar mais
Veja também: Função quadrática (guia completo) e Vértice da parábola.