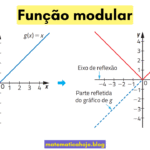
Função sobrejetiva
Definição, testes práticos, exemplos e exercícios resolvidos — tudo em uma página.
Uma função \(f:A\to B\) é sobrejetiva (ou sobrejeção) quando todo elemento do contradomínio \(B\) é imagem de algum elemento do domínio \(A\). Em notação:
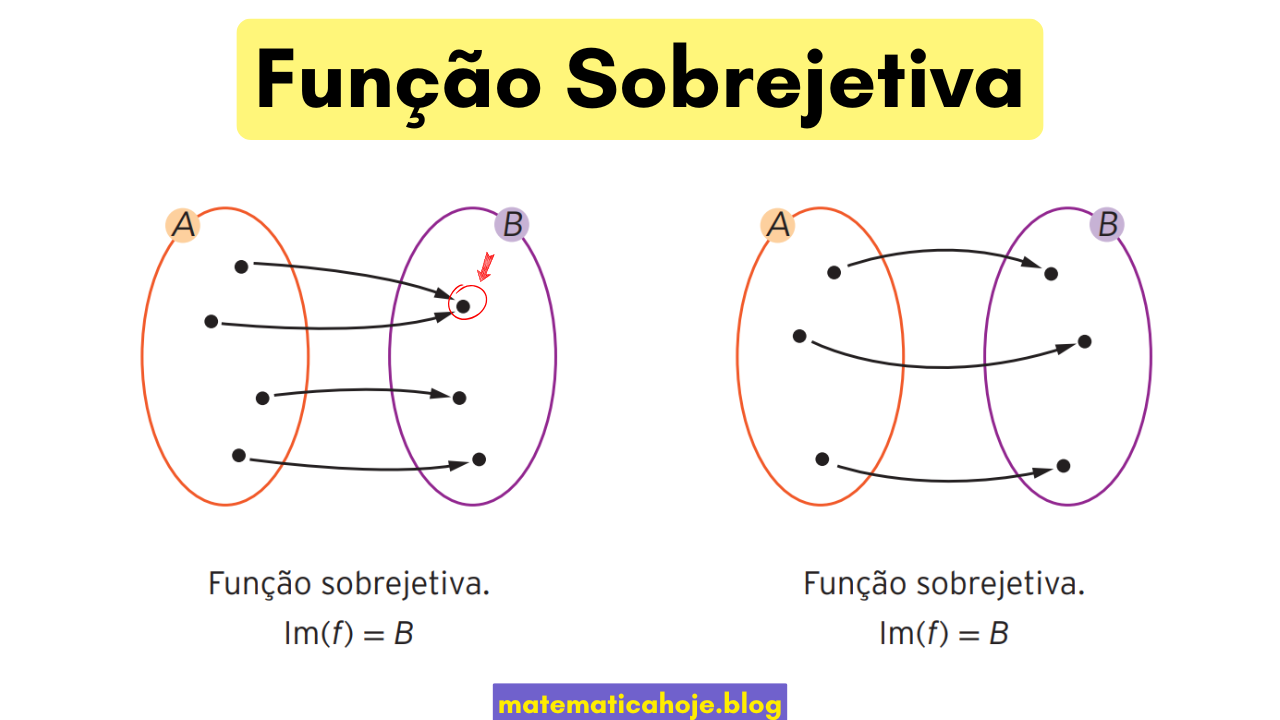
Teste da cobertura (visual e lógico)
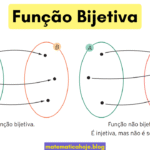
- Visual (diagrama de setas): todo ponto de \(B\) recebe pelo menos uma seta.
- Lógico: dado \(y\in B\), você consegue resolver \(f(x)=y\) e obter algum \(x\in A\)? Se sim, para todo \(y\), então \(f\) é sobrejetiva.
- Cardinalidade (finito): se \(|A|<|B|\), não pode ser sobrejetiva. Se \(|A|\ge |B|\), é apenas condição necessária, não suficiente.
Dicas e fatos rápidos
- Escolha do contradomínio importa: \(e^x\) não é sobrejetiva em \(\mathbb{R}\), mas é sobrejetiva em \((0,\infty)\).
- Contínuas em \(\mathbb{R}\) com \(\lim_{x\to-\infty}f(x)=-\infty\) e \(\lim_{x\to\infty}f(x)=\infty\) são sobrejetivas em \(\mathbb{R}\) (ex.: polinômios de grau ímpar).
- Composição: se \(f\) e \(g\) são sobrejetivas, então \(g\circ f\) é sobrejetiva; se \(g\circ f\) é sobrejetiva, então \(g\) é sobrejetiva.
- Inversa à direita: \(f\) é sobrejetiva \(\iff\) existe \(h:B\to A\) tal que \(f\circ h=\operatorname{id}_B\).
Exemplos resolvidos
1) Linear
\(f(x)=ax+b\) com \(a\neq0\) é sobrejetiva em \(\mathbb{R}\). Dado \(y\in\mathbb{R}\), \(x=\dfrac{y-b}{a}\) resolve \(f(x)=y\).
2) Quadrática
\(g(x)=x^2\) não é sobrejetiva em \(\mathbb{R}\) (pois \(g(x)\ge0\)), mas é sobrejetiva em \([0,\infty)\). Para \(y\ge0\), escolha \(x=\sqrt{y}\) ou \(x=-\sqrt{y}\).
3) Exponencial
\(h(x)=e^x\) tem \(\operatorname{Im}(h)=(0,\infty)\). É sobrejetiva em \((0,\infty)\) e não sobrejetiva em \(\mathbb{R}\).
4) Seno
\(\sin x\) é sobrejetiva em \([-1,1]\) (imagem de \(\mathbb{R}\) é exatamente \([-1,1]\)).
5) Transformação de Möbius
\(F(x)=\dfrac{ax+b}{cx+d}\) com \(ad-bc\neq0\). No domínio \(\mathbb{R}\setminus\{-d/c\}\), a imagem é \(\mathbb{R}\setminus\{a/c\}\). Assim, \(F:\mathbb{R}\setminus\{-d/c\}\to\mathbb{R}\setminus\{a/c\}\) é sobrejetiva, mas não é sobrejetiva em \(\mathbb{R}\).
Quadro-resumo
| Ferramenta | Ideia | Exemplo |
|---|---|---|
| Resolver \(f(x)=y\) | Para todo \(y\in B\), encontre ao menos um \(x\in A\) | \(ax+b=y\Rightarrow x=\dfrac{y-b}{a}\) |
| Imagem conhecida | Compare \(\operatorname{Im}(f)\) com \(B\) | \(e^x\Rightarrow(0,\infty)\) |
| Limites/IVT | Se contínua e cobre todos os valores por limites | Polinômio grau ímpar \(\Rightarrow \mathbb{R}\) |
| Cardinalidade | \(|A|<|B|\Rightarrow\) impossível (finito) | 3 elementos \(\nrightarrow\) 4 elementos |
| Composição | \(f,g\) sobrejetivas \(\Rightarrow g\circ f\) sobrejetiva | Projeção + projeção |
Exercícios (múltipla escolha) com solução
1) Classifique quanto à sobrejetividade no contradomínio indicado:
- \(f(x)=2x-3\) com \(B=\mathbb{R}\).
- \(g(x)=x^2\) com \(B=\mathbb{R}\).
- \(h(x)=e^x\) com \(B=(0,\infty)\).
- \(p(x)=|x|\) com \(B=[0,\infty)\).
- Somente \(f\) e \(h\) são sobrejetivas.
- Somente \(g\) e \(p\) são sobrejetivas.
- \(f\), \(h\) e \(p\) são sobrejetivas; \(g\) não.
- Todos são sobrejetivas.
Ver solução
2) \(\sin x\) é sobrejetiva em qual contradomínio?
- \(\mathbb{R}\)
- \([-1,1]\)
- \((0,1)\)
- \((-\infty,0]\)
Ver solução
3) Seja \(f(x)=x^3+2x\) em \(\mathbb{R}\). É sobrejetiva em \(\mathbb{R}\)?
- Não, pois \(f(x)\ge0\).
- Sim, por continuidade e limites \(\pm\infty\).
- Somente em \([0,\infty)\).
- Somente se \(x\ge0\).
Ver solução
4) A função piso \(\lfloor x\rfloor:\mathbb{R}\to\mathbb{Z}\) é:
- Sobrejetiva e injetiva.
- Sobrejetiva e não injetiva.
- Injetiva e não sobrejetiva.
- Nem injetiva nem sobrejetiva.
Ver solução
5) Se \(g\circ f:A\to C\) é sobrejetiva, qual afirmação é verdadeira?
- \(f\) é sobrejetiva.
- \(g\) é sobrejetiva.
- Ambas \(f\) e \(g\) são sobrejetivas.
- Nenhuma conclusão.
Ver solução
6) \(F(x)=\dfrac{ax+b}{cx+d}\) (\(ad-bc\neq0\)). Em qual contradomínio \(B\) ela é sobrejetiva?
- \(B=\mathbb{R}\)
- \(B=\mathbb{R}\setminus\{a/c\}\)
- \(B=\mathbb{R}\setminus\{-d/c\}\)
- Em nenhum
Ver solução
Continue estudando (links internos)
• Função injetiva
• Gráfico de uma Função
• Funções crescente/decrescente/constante
• Plano Cartesiano
• ENEM Matemática
• Coleção 10 eBooks de Matemática
• eBook Fórmulas Matemática
• Banco de Questões