Confira uma seleção de 5 questões resolvidas que abordam os principais conceitos de funções matemáticas e suas representações no plano cartesiano. Nesta lista, você encontrará exercícios sobre coordenadas de pontos, pares ordenados equivalentes, domínio e imagem de funções reais, gráficos com regiões de pontuação e variação de temperatura ao longo do tempo. Cada questão vem acompanhada de enunciado completo, imagem ilustrativa e resolução comentada passo a passo – ideal para estudantes do ensino fundamental II, médio e para revisão em concursos. Domine os gráficos e interprete funções com confiança!
🧠 Mapas Mentais de MatemáticaConteúdo: Coordenadas no Plano Cartesiano
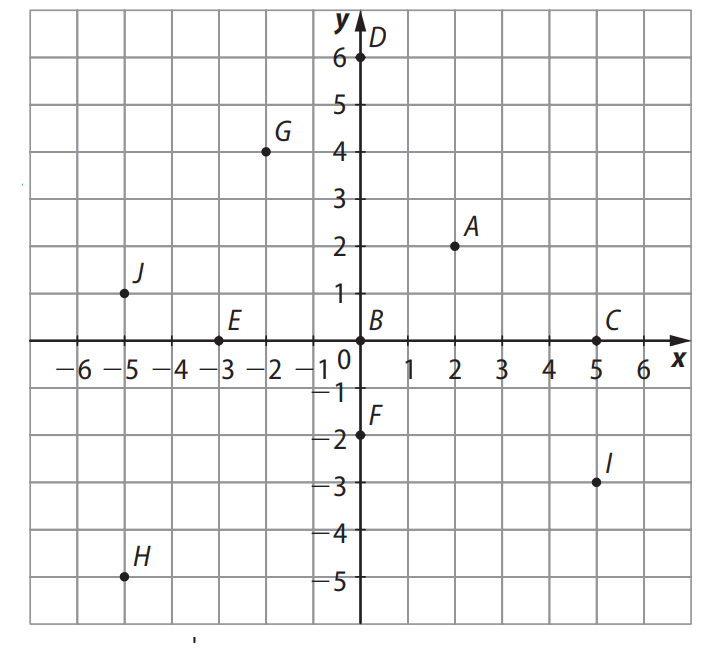
Questão 13. Determine as coordenadas dos pontos indicados na figura.
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Devemos identificar as coordenadas de cada ponto rotulado (A até J) observando suas posições nos eixos \(x\) e \(y\).
1) Localizando os pontos no plano:
- A: $$ (2,\ 2) $$
- B: $$ (0,\ 0) $$
- C: $$ (5,\ 0) $$
- D: $$ (0,\ 6) $$
- E: $$ (-3,\ 0) $$
- F: $$ (0,\ -2) $$
- G: $$ (-2,\ 4) $$
- H: $$ (-5,\ -5) $$
- I: $$ (4,\ -3) $$
- J: $$ (-5,\ 1) $$
2) Conclusão:
As coordenadas foram determinadas com base na contagem dos quadrados a partir da origem \((0,0)\), respeitando o sinal dos eixos.
🧠 Mapas Mentais de MatemáticaConteúdo: Pares ordenados e igualdade de pontos no plano cartesiano
Questão 14. Dados os pares ordenados \( (2a – 3,\ b + 2) \) e \( (5a – 1,\ 2b – 3) \) e sabendo que ambos representam o mesmo ponto no sistema cartesiano, quais são os valores de \( a \) e \( b \)?
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Se dois pares ordenados representam o mesmo ponto, então suas coordenadas correspondentes devem ser iguais.
1) Igualando as coordenadas correspondentes:
Primeira coordenada:
$$ 2a – 3 = 5a – 1 $$
Segunda coordenada:
$$ b + 2 = 2b – 3 $$
2) Resolvendo a equação para \( a \):
$$ 2a – 3 = 5a – 1 $$
$$ -3 + 1 = 5a – 2a $$
$$ -2 = 3a \Rightarrow a = -\frac{2}{3} $$
3) Resolvendo a equação para \( b \):
$$ b + 2 = 2b – 3 $$
$$ 2 + 3 = 2b – b $$
$$ 5 = b $$
✅ Conclusão:
- Valor de \( a \): $$ a = -\frac{2}{3} $$
- Valor de \( b \): $$ b = 5 $$
Conteúdo: Coordenadas, regiões no plano cartesiano e pontuação
Questão 15. (OBMEP) Manoel testa sua pontaria lançando 5 flechas que atingiram o alvo nos pontos A, B, C, D e E, de coordenadas:
- A = \( (1,\ -1) \)
- B = \( (2{,}5,\ 1) \)
- C = \( (-1,\ 4) \)
- D = \( (-4,\ -4) \)
- E = \( (6,\ 5) \)
A imagem mostra as regiões de pontuação do alvo. Cada cor representa uma pontuação diferente conforme a distância da origem:
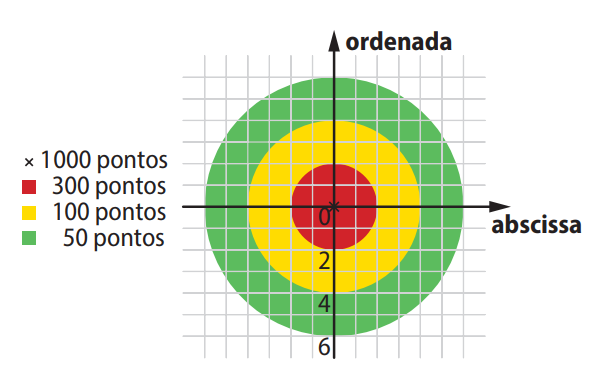 a) Marque os pontos A, B, C, D e E.
b) Quantas flechas ele acertou no interior do
menor círculo?
c) Ao todo, quantos pontos Manoel fez?
a) Marque os pontos A, B, C, D e E.
b) Quantas flechas ele acertou no interior do
menor círculo?
c) Ao todo, quantos pontos Manoel fez?🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Precisamos determinar a pontuação total de Manoel observando em qual região cada flecha caiu com base nas coordenadas fornecidas e nas regiões circulares do alvo.
1) Determinar a distância de cada ponto até a origem (0, 0):
- A: \( \sqrt{1^2 + (-1)^2} = \sqrt{2} \approx 1{,}41 \) → Região vermelha → 1000 pontos
- B: \( \sqrt{(2{,}5)^2 + 1^2} = \sqrt{6{,}25 + 1} = \sqrt{7{,}25} \approx 2{,}69 \) → Região amarela → 300 pontos
- C: \( \sqrt{(-1)^2 + 4^2} = \sqrt{1 + 16} = \sqrt{17} \approx 4{,}12 \) → Região verde → 50 pontos
- D: \( \sqrt{(-4)^2 + (-4)^2} = \sqrt{16 + 16} = \sqrt{32} \approx 5{,}66 \) → Região verde → 50 pontos
- E: \( \sqrt{6^2 + 5^2} = \sqrt{36 + 25} = \sqrt{61} \approx 7{,}81 \) → Fora do alvo → 0 pontos
2) Contabilizar quantas flechas atingiram o menor círculo:
Somente o ponto A está no círculo vermelho (menor círculo).
Resposta (b): 1 flecha
3) Somar a pontuação total:
\( 1000 + 300 + 50 + 50 + 0 = 1400 \) pontos
Resposta (c): 1400 pontos
✅ Conclusão:
- b) 1 flecha no menor círculo
- c) Total de pontos: $$ \boxed{1400} $$
Conteúdo: Domínio e Imagem de Funções Reais
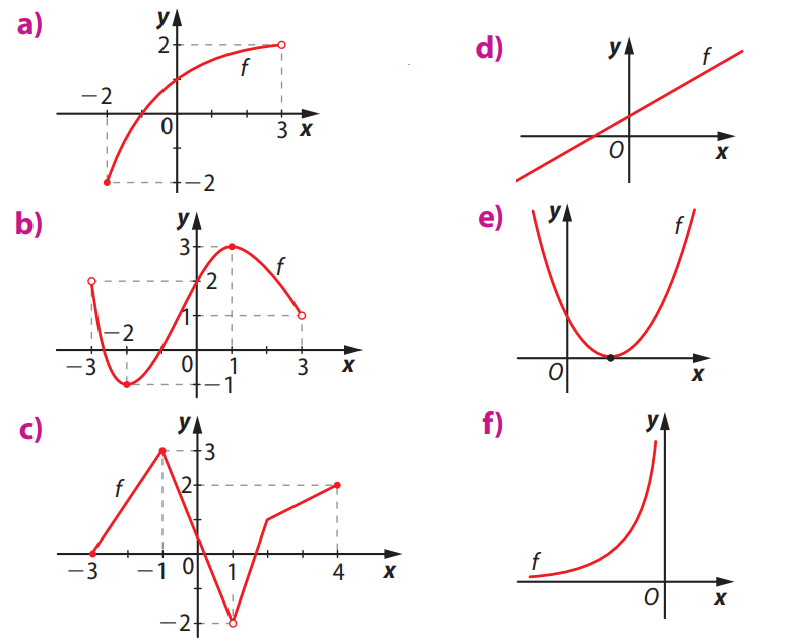
Questão 16. Os esboços dos gráficos a seguir representam funções reais de variável real. Observando-os, determine o domínio \( D(f) \) e o conjunto imagem \( \text{Im}(f) \) de cada função.
🔍 Ver solução passo a passo
Função a)
Domínio: $$ D(f) = \{ x \in \mathbb{R} \mid -2 \leq x \leq 3 \} $$
Imagem: $$ \text{Im}(f) = \{ y \in \mathbb{R} \mid -2 \leq y \leq 2 \} $$
Função b)
Domínio: $$ D(f) = \{ x \in \mathbb{R} \mid -3 < x < 3 \} $$
Imagem: $$ \text{Im}(f) = \{ y \in \mathbb{R} \mid -1 \leq y \leq 3 \} $$
Função c)
Domínio: $$ D(f) = \{ x \in \mathbb{R} \mid -3 \leq x \leq 4 \text{ e } x \neq 1 \} $$
Imagem: $$ \text{Im}(f) = \{ y \in \mathbb{R} \mid -2 \leq y \leq 3 \} $$
Função d)
Domínio: $$ D(f) = \mathbb{R} $$
Imagem: $$ \text{Im}(f) = \mathbb{R} $$
Função e)
Domínio: $$ D(f) = \mathbb{R} $$
Imagem: $$ \text{Im}(f) = \{ y \in \mathbb{R} \mid y \geq 0 \} $$
Função f)
Domínio: $$ D(f) = \{ x \in \mathbb{R} \mid x < 0 \} $$
Imagem: $$ \text{Im}(f) = \{ y \in \mathbb{R} \mid y > 0 \} $$
✅ Conclusão:
- Domínio refere-se aos valores possíveis para \( x \)
- Imagem refere-se aos valores resultantes de \( f(x) \)
Conteúdo: Leitura e interpretação de gráficos de funções
Questão 17. (UFV-MG) O gráfico a seguir ilustra a evolução da temperatura \( T \) (°C), em uma região, ao longo de um período de 24 horas.
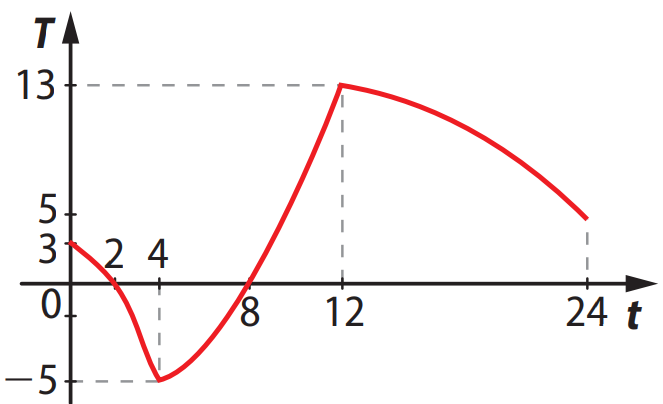 Determine:
a) os horários em que a temperatura atinge
0 °C; às 2 h e às 8 h
b) o intervalo de variação da temperatura ao
longo das 24 horas;
c) os intervalos de tempo em que a temperatura é positiva.
Determine:
a) os horários em que a temperatura atinge
0 °C; às 2 h e às 8 h
b) o intervalo de variação da temperatura ao
longo das 24 horas;
c) os intervalos de tempo em que a temperatura é positiva.
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Precisamos analisar o gráfico da função \( T(t) \), que representa a temperatura ao longo do tempo em horas, para determinar:
- Quando \( T(t) = 0^\circ \text{C} \);
- O intervalo de variação da temperatura;
- Os intervalos em que \( T(t) > 0 \).
a) Horários em que a temperatura é 0 ºC:
Observando o gráfico, a temperatura cruza o eixo \( x \) nos pontos:
$$ t = 2\text{h} \quad \text{e} \quad t = 8\text{h} $$
b) Intervalo de variação da temperatura:
O valor mínimo é \( -5^\circ \text{C} \) e o máximo é \( 13^\circ \text{C} \).
$$ \text{Variação: } [-5,\ 13] $$
c) Intervalo de tempo com temperatura positiva:
A função é positiva quando está acima do eixo \( x \), ou seja:
$$ t \in (0,\ 2) \cup (8,\ 24) $$
✅ Conclusão:
- a) Temperatura igual a 0 °C: às 2h e às 8h
- b) Intervalo de variação: de −5 °C a 13 °C
- c) Intervalos com temperatura positiva: de 0h às 2h e de 8h às 24h




























