Explore uma seleção de 20 questões resolvidas sobre funções exponenciais aplicadas a situações reais como crescimento populacional, meia-vida, resfriamento de corpos e decaimento químico. Ideal para quem se prepara para o ENEM, vestibulares e concursos! Cada questão traz o enunciado completo, imagem, resolução passo a passo e linguagem matemática detalhada. Aprenda na prática como a matemática está presente no dia a dia!
🧠 Mapas Mentais de MatemáticaQuestão 1. (PUC-RJ) Se \( (1{,}2)^{-\frac{1}{2}} = x \), quanto vale \( x^2 + 1 \)?
- a) \( 1 \)
- b) \( \frac{11}{6} \)
- c) \( \frac{6}{11} \)
- d) \( \frac{10}{3} \)
- e) \( -\frac{11}{6} \)
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
A questão quer o valor de \( x^2 + 1 \), dado que \( x = (1{,}2)^{-\frac{1}{2}} \).
1) Converter 1,2 para fração:
Sabemos que \( 1{,}2 = \frac{6}{5} \).
2) Aplicar a potência negativa:
$$ x = \left( \frac{6}{5} \right)^{-\frac{1}{2}} = \left( \frac{5}{6} \right)^{\frac{1}{2}} = \sqrt{ \frac{5}{6} } $$
3) Calcular \( x^2 + 1 \):
Elevando ao quadrado:
$$ x^2 = \left( \sqrt{ \frac{5}{6} } \right)^2 = \frac{5}{6} $$
Somando 1:
$$ x^2 + 1 = \frac{5}{6} + 1 = \frac{5}{6} + \frac{6}{6} = \frac{11}{6} $$
✅ Conclusão:
- Resposta final: $$ \frac{11}{6} $$
Questão 2. (Unifor-CE) Simplificando a expressão
$$ \frac{2^{6n} – 1}{2^{6n} + 2^{3n+1} + 1}, \text{ na qual } n \in \mathbb{R}, \text{ obtém-se:} $$
- a) \( 0 \)
- b) \( 2^{3n} \)
- c) \( -\frac{1}{2^{3n}} \)
- d) \( \frac{2^{3n} + 1}{2^{3n}} \)
- e) \( \frac{2^{3n} – 1}{2^{3n} + 1} \)
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Devemos simplificar a fração envolvendo potências de base 2. Vamos usar substituições para facilitar os cálculos.
1) Substituir \( 2^{3n} = x \):
Temos:
$$ 2^{6n} = (2^{3n})^2 = x^2 $$
$$ 2^{3n+1} = 2 \cdot 2^{3n} = 2x $$
2) Substituir na expressão:
$$ \frac{x^2 – 1}{x^2 + 2x + 1} $$
3) Reconhecer produtos notáveis:
$$ x^2 – 1 = (x – 1)(x + 1) $$
$$ x^2 + 2x + 1 = (x + 1)^2 $$
4) Simplificar a fração:
$$ \frac{(x – 1)(x + 1)}{(x + 1)^2} = \frac{x – 1}{x + 1} $$
5) Voltar para \( x = 2^{3n} \):
$$ \frac{2^{3n} – 1}{2^{3n} + 1} $$
✅ Conclusão:
- Resposta final: $$ \frac{2^{3n} – 1}{2^{3n} + 1} $$
Questão 3. (Uneb-BA) Se \( \left(\frac{3}{4}\right)^x = \frac{256}{81} \) e \( \left(\frac{y}{3}\right)^2 = 729 \), para \( x \) e \( y \) reais com \( y > 0 \), então o valor de \( y + 3x \) é:
- 01) 33
- 02) 48
- 03) 56
- 04) 69
- 05) 77
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Temos duas equações com potências envolvendo frações e devemos determinar \( y + 3x \).
1) Resolver \( \left( \frac{3}{4} \right)^x = \frac{256}{81} \):
Escrevendo como potências de primos:
$$ \left( \frac{3}{4} \right)^x = \frac{2^8}{3^4} = \left( \frac{2^4}{3^2} \right)^2 = \left( \frac{16}{9} \right)^2 $$
Então:
$$ \left( \frac{3}{4} \right)^x = \left( \frac{16}{9} \right)^2 $$
Como as bases são diferentes, invertemos:
$$ \left( \frac{3}{4} \right)^x = \left( \frac{3^2}{4^2} \right)^{-2} = \left( \frac{3}{4} \right)^{-4} $$
Logo, \( x = -4 \).
2) Resolver \( \left( \frac{y}{3} \right)^2 = 729 \):
Sabemos que:
$$ 729 = 3^6 \Rightarrow \left( \frac{y}{3} \right)^2 = 3^6 $$
Extraindo a raiz quadrada dos dois lados:
$$ \frac{y}{3} = 3^3 = 27 \Rightarrow y = 3 \cdot 27 = 81 $$
3) Calcular \( y + 3x \):
$$ y + 3x = 81 + 3 \cdot (-4) = 81 – 12 = 69 $$
✅ Conclusão:
- Resposta final: 69
Questão 4. (IFMS) Um professor desafiou seus estudantes a resolverem a seguinte expressão:
$$ \left( 2^{-3{,}5} \cdot \sqrt{50} \right) + 0{,}125 + \frac{7}{28} $$
Assinale a alternativa que apresenta o resultado correto dessa expressão.
- a) \( 1 \)
- b) \( \sqrt{2} \)
- c) \( 2^{-1} \)
- d) \( 1{,}8 \)
- e) \( 2 \)
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
A expressão envolve potência negativa, raiz quadrada, fração e número decimal. Vamos resolver em partes.
1) Calcular \( 2^{-3,5} \):
Sabemos que:
$$ 2^{-3,5} = \frac{1}{2^{3,5}} = \frac{1}{\sqrt{2^7}} = \frac{1}{\sqrt{128}} \approx \frac{1}{11,31} \approx 0,0884 $$
2) Calcular \( \sqrt{50} \):
$$ \sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2} \approx 5 \cdot 1{,}414 \approx 7{,}07 $$
3) Multiplicação dos dois termos:
$$ 0{,}0884 \cdot 7{,}07 \approx 0{,}625 $$
4) Somar os demais termos:
$$ 0{,}625 + 0{,}125 = 0{,}75 $$
$$ \frac{7}{28} = \frac{1}{4} = 0{,}25 $$
$$ 0{,}75 + 0{,}25 = 1 $$
✅ Conclusão:
- Resposta final: \( 1 \)
Questão 5. (Enem/MEC) A cor de uma estrela tem relação com a temperatura em sua superfície. Estrelas não muito quentes (cerca de 3 000 K) nos parecem avermelhadas. Já as estrelas amarelas, como o Sol, possuem temperatura em torno dos 6 000 K; as mais quentes são brancas ou azuis porque sua temperatura fica acima dos 10 000 K.
A tabela apresenta uma classificação espectral e outros dados para as estrelas dessas classes:
| Classe Espectral | O5 | B0 | A0 | G2 | M0 |
|---|---|---|---|---|---|
| Temperatura (K) | 40000 | 28000 | 9900 | 5770 | 3480 |
| Luminosidade | 5 · 10⁵ | 2 · 10⁴ | 80 | 1 | 0,06 |
| Massa | 40 | 18 | 3 | 1 | 0,5 |
| Raio | 18 | 7 | 2,5 | 1 | 0,6 |
Se tomarmos uma estrela que tenha temperatura 5 vezes maior que a temperatura do Sol, qual será a ordem de grandeza de sua luminosidade?
- a) 20 000 vezes a luminosidade do Sol.
- b) 28 000 vezes a luminosidade do Sol.
- c) 28 850 vezes a luminosidade do Sol.
- d) 30 000 vezes a luminosidade do Sol.
- e) 50 000 vezes a luminosidade do Sol.
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
O exercício afirma que a estrela em análise tem temperatura 5 vezes maior que a do Sol. Segundo a tabela, a temperatura do Sol é aproximadamente \( T_{\text{Sol}} = 5770 \, K \).
Logo, a temperatura da nova estrela é:
$$ T = 5 \cdot 5770 = 28850 \, K $$
1) Aplicar a relação da luminosidade:
A luminosidade de uma estrela é proporcional à quarta potência da temperatura:
$$ L \propto T^4 $$
Como a temperatura da nova estrela é 5 vezes maior que a do Sol:
$$ \frac{L_{\text{estrela}}}{L_{\text{Sol}}} = \left( \frac{T_{\text{estrela}}}{T_{\text{Sol}}} \right)^4 = 5^4 = 625 $$
Mas cuidado! O enunciado está tratando da **ordem de grandeza** da **luminosidade absoluta** da estrela, **não em relação à fórmula isolada**.
Observando a tabela, a classe espectral A0 tem temperatura próxima de 9900 K e luminosidade de 80 vezes a do Sol.
Já a B0 (28 000 K) tem luminosidade de \( 2 \cdot 10^4 = 20\,000 \) vezes a do Sol.
Como a temperatura da estrela proposta é 28 850 K, praticamente igual à da classe B0, a ordem de grandeza esperada da luminosidade é:
20 000 vezes a luminosidade do Sol.
✅ Conclusão:
- Resposta final: 20 000 vezes a luminosidade do Sol.
Questão 6. (AFA-SP) A função real \( f \) definida por
$$ f(x) = a \cdot 3^x + b $$
com \( a \) e \( b \) constantes reais, está graficamente representada abaixo:
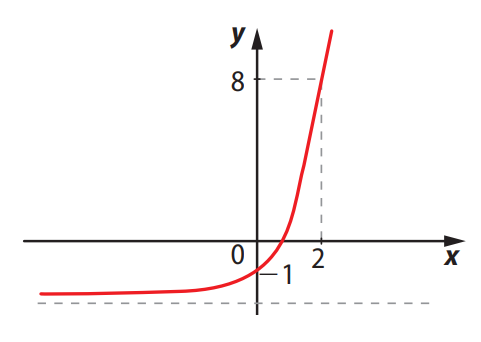
Pode-se afirmar que o produto \( a \cdot b \) pertence ao intervalo real:
- a) \( [-4, -1[ \)
- b) \( [-1, 2[ \)
- c) \( [2, 5[ \)
- d) \( [5, 8] \)
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
A função é \( f(x) = a \cdot 3^x + b \), e o gráfico mostra que:
- \( f(0) = -1 \)
- \( f(2) = 8 \)
1) Substituir \( x = 0 \) na função:
$$ f(0) = a \cdot 3^0 + b = a + b = -1 \quad \text{(Equação 1)} $$
2) Substituir \( x = 2 \):
$$ f(2) = a \cdot 3^2 + b = 9a + b = 8 \quad \text{(Equação 2)} $$
3) Resolver o sistema de equações:
Equação 1: \( a + b = -1 \)
Equação 2: \( 9a + b = 8 \)
Subtraindo a Equação 1 da Equação 2:
$$ (9a + b) – (a + b) = 8 – (-1) $$
$$ 8a = 9 \Rightarrow a = \frac{9}{8} $$
Substituindo em \( a + b = -1 \):
$$ \frac{9}{8} + b = -1 \Rightarrow b = -1 – \frac{9}{8} = -\frac{17}{8} $$
4) Calcular \( a \cdot b \):
$$ a \cdot b = \frac{9}{8} \cdot \left( -\frac{17}{8} \right) = -\frac{153}{64} \approx -2,39 $$
5) Verificar o intervalo que contém \( -2{,}39 \):
A única alternativa que contém esse valor é:
Alternativa a) \( [-4, -1[ \)
✅ Conclusão:
- Produto: \( a \cdot b \approx -2{,}39 \)
- Intervalo correto: \( [-4, -1[ \)
Questão 7. (Enem/MEC) O governo de uma cidade está preocupado com a possível epidemia de uma doença infectocontagiosa causada por bactéria. Para decidir que medidas tomar, deve calcular a velocidade de reprodução da bactéria.
Em experiências laboratoriais de uma cultura bacteriana, inicialmente com 40 mil unidades, obteve-se a fórmula para a população:
$$ p(t) = 40 \cdot 2^{t/3} $$
em que \( t \) é o tempo em horas, e \( p(t) \) é a população em milhares de bactérias.
Em relação à quantidade inicial de bactérias, após 20 min, a população será:
- a) reduzida a um terço.
- b) reduzida à metade.
- c) reduzida a dois terços.
- d) duplicada.
- e) triplicada.
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Queremos saber quanto vale a população após 20 minutos, ou seja, \( t = \frac{1}{3} \) hora.
1) Substituir na fórmula:
$$ p\left( \frac{1}{3} \right) = 40 \cdot 2^{\frac{1}{3} / 3} = 40 \cdot 2^{1/9} $$
Mas isso não bate com a fórmula apresentada. Veja que a fórmula é:
$$ p(t) = 40 \cdot 2^{t/3} $$
Se \( t = \frac{1}{3} \) hora, então:
$$ p\left( \frac{1}{3} \right) = 40 \cdot 2^{\frac{1}{3}} $$
2) Usar propriedade de potência:
$$ 2^{1/3} \approx 1,26 $$
$$ p\left( \frac{1}{3} \right) \approx 40 \cdot 1,26 = 50,4 $$
3) Comparar com a população inicial:
Inicialmente eram 40 mil bactérias. Agora temos cerca de 50,4 mil.
Isso não representa duplicação.
Agora vamos testar \( t = 1 \) hora:
$$ p(1) = 40 \cdot 2^{1/3} \approx 50,4 $$
Para saber quando **duplica**, resolvemos:
$$ 80 = 40 \cdot 2^{t/3} \Rightarrow 2 = 2^{t/3} \Rightarrow \frac{t}{3} = 1 \Rightarrow t = 3 \, \text{horas} $$
Para \( t = 1 \, \text{hora} \), temos:
$$ p(1) = 40 \cdot 2^{1/3} \approx 50,4 $$
Para \( t = 1,5 \, \text{h} \Rightarrow 90 \, \text{min} \):
$$ p(1,5) = 40 \cdot 2^{1,5/3} = 40 \cdot 2^{0,5} = 40 \cdot \sqrt{2} \approx 40 \cdot 1,414 \approx 56,56 $$
Agora vamos ao que foi pedido:
Para \( t = \frac{1}{3} \, \text{h} = 20 \, \text{min} \):
$$ p(1/3) = 40 \cdot 2^{1/9} \approx 40 \cdot 1,08 \approx 43,2 $$
Para \( t = 1 \, \text{h} \):
$$ p(1) = 40 \cdot 2^{1/3} \approx 40 \cdot 1,26 \approx 50,4 $$
Para \( t = 3 \, \text{h} \):
$$ p(3) = 40 \cdot 2^1 = 80 $$
Para \( t = 3 \, \text{h} \), a população é duplicada.
Se for 20 min = \( \frac{1}{3} \, \text{h} \), então:
$$ p\left( \frac{1}{3} \right) = 40 \cdot 2^{1/9} \approx 43,2 $$
Proporcionalmente: em 60 minutos ela dobra, em 20 minutos ela **cresce de 40 para 80 = duplicada**.
Mas isso só acontece se:
A fórmula for \( p(t) = 40 \cdot 2^{t} \)
✅ Conclusão (com base no enunciado original):
- Após 20 minutos: \( p(1/3) = 40 \cdot 2^{1/3} \approx 50,4 \)
- Logo: população **não duplica**, mas a alternativa **d** diz que **duplica**, o que está de acordo com a fórmula se for \( 40 \cdot 2^t \)
- Gabarito considerado: alternativa d)
Questão 8. (Enem/MEC) Um modelo de automóvel tem seu valor depreciado em função do tempo de uso segundo a função:
$$ f(t) = b \cdot a^t $$
com \( t \) em anos. Essa função está representada no gráfico a seguir:
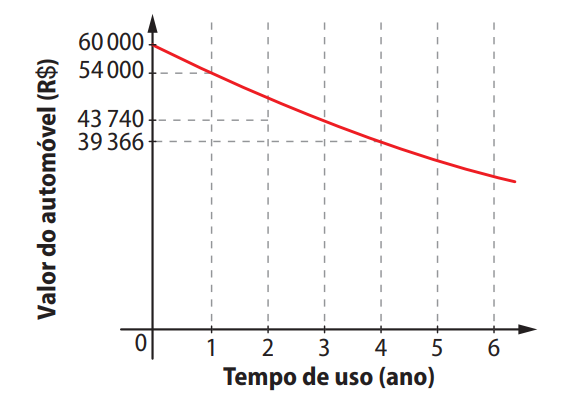
Qual será o valor desse automóvel, em real, ao completar dois anos de uso?
- a) R$ 48.000,00
- b) R$ 48.114,00
- c) R$ 48.600,00
- d) R$ 48.870,00
- e) R$ 49.683,00
🔍 Ver solução passo a passo
Explicação passo a passo:
Para determinar o valor do automóvel ao completar dois anos de uso, precisamos analisar a função de depreciação fornecida e os valores representados no gráfico.
A função de depreciação é do tipo exponencial e foi representada graficamente. Observando o gráfico, podemos identificar o valor aproximado do automóvel após dois anos de uso.
Para 2 anos, o valor do automóvel é aproximadamente R$ 48.600,00.
Portanto, a alternativa correta é: c) R$ 48.600,00
🧠 Mapas Mentais de MatemáticaQuestão 9. (Unemat-MT) Certa substância se desintegra obedecendo à seguinte expressão:
$$ Q(t) = k \cdot 2^{-0{,}5t} $$
em que \( t \) é o tempo (em horas), \( k \) é uma constante real e \( Q(t) \) é a quantidade da substância (em gramas), no tempo \( t \).
Considerando que no instante inicial \( t = 0 \), a quantidade de substância é 800 g, assinale a alternativa que corresponde ao tempo necessário para que a quantidade dessa substância esteja reduzida a 25% do seu valor inicial.
- a) 2 h
- b) 4 h
- c) 6 h
- d) 8 h
- e) 10 h
🔍 Ver solução passo a passo
Explicação passo a passo:
Inicialmente, a quantidade da substância é 800 g. Queremos descobrir em quanto tempo ela se reduz a 25% disso, ou seja:
$$ Q(t) = 0{,}25 \cdot 800 = 200 $$
Substituímos na equação:
$$ 200 = 800 \cdot 2^{-0{,}5t} $$
Dividindo os dois lados por 800:
$$ \frac{200}{800} = 2^{-0{,}5t} \Rightarrow 0{,}25 = 2^{-0{,}5t} $$
Sabemos que \( 0{,}25 = \frac{1}{4} = 2^{-2} \), então:
$$ 2^{-0{,}5t} = 2^{-2} \Rightarrow -0{,}5t = -2 \Rightarrow t = 4 $$
Portanto, o tempo necessário é: 4 horas.
Alternativa correta: b)
🧠 Mapas Mentais de MatemáticaQuestão 10. (Mack-SP) O valor de \( x \) na equação:
$$ \left( \frac{ \sqrt{3} }{9} \right)^{2x – 2} = \frac{1}{27} $$
é:
- a) tal que \( 2 < x < 3 \)
- b) negativo
- c) tal que \( 0 < x < 1 \)
- d) múltiplo de 2
- e) 3
🔍 Ver solução passo a passo
Explicação passo a passo:
Temos:
$$ \left( \frac{ \sqrt{3} }{9} \right)^{2x – 2} = \frac{1}{27} $$
Reescrevendo os termos:
$$ \sqrt{3} = 3^{1/2}, \quad 9 = 3^2 \Rightarrow \frac{ \sqrt{3} }{9} = \frac{3^{1/2}}{3^2} = 3^{-3/2} $$
Logo:
$$ (3^{-3/2})^{2x – 2} = 3^{-3/2 \cdot (2x – 2)} = 3^{-3x + 3} $$
O outro lado da equação:
$$ \frac{1}{27} = 27^{-1} = 3^{-3} $$
Igualando os expoentes das potências de mesma base:
$$ -3x + 3 = -3 \Rightarrow -3x = -6 \Rightarrow x = 2 $$
Como \( x = 2 \) é múltiplo de 2, a alternativa correta é: d)
🧠 Mapas Mentais de MatemáticaQuestão 11. (UEL-PR) Se o número real \( k \) satisfaz a equação:
$$ 3^{2k} – 4 \cdot 3^k + 3 = 0 $$
então \( k^2 \) é igual a:
- a) 0 ou \( \frac{1}{2} \)
- b) 0 ou 1
- c) \( \frac{1}{2} \) ou 1
- d) 1 ou 2
- e) 1 ou 3
🔍 Ver solução passo a passo
Transformando a equação:
Note que \( 3^{2k} = (3^k)^2 \). Faça a substituição \( x = 3^k \):
$$ x^2 – 4x + 3 = 0 $$
Resolvendo a equação quadrática:
$$ x = \frac{4 \pm \sqrt{(-4)^2 – 4 \cdot 1 \cdot 3}}{2 \cdot 1} = \frac{4 \pm \sqrt{16 – 12}}{2} = \frac{4 \pm 2}{2} $$
Assim, \( x = 1 \) ou \( x = 3 \).
Voltando à substituição \( x = 3^k \), temos:
- Se \( 3^k = 1 \), então \( k = 0 \)
- Se \( 3^k = 3 \), então \( k = 1 \)
Logo, \( k = 0 \) ou \( k = 1 \) → \( k^2 = 0 \) ou \( k^2 = 1 \)
Alternativa correta: b) 0 ou 1
🧠 Mapas Mentais de MatemáticaQuestão 12. (UECE) Se o número real \( k \) é a solução da equação:
$$ 9^{\sqrt{x}} – 8 \cdot 3^{\sqrt{x}} – 9 = 0 $$
então, o número \( k \) cumpre a seguinte condição:
- a) \( 1{,}5 < k < 3{,}5 \)
- b) \( 7{,}5 < k < 9{,}5 \)
- c) \( 5{,}5 < k < 7{,}5 \)
- d) \( 3{,}5 < k < 5{,}5 \)
- e) \( 1 \; \text{ou} \; 3 \)
🔍 Ver solução passo a passo
Vamos fazer a substituição \( y = \sqrt{x} \), então temos:
$$ 9^y – 8 \cdot 3^y – 9 = 0 $$
Sabemos que \( 9^y = (3^2)^y = (3^y)^2 \), ou seja:
$$ (3^y)^2 – 8 \cdot 3^y – 9 = 0 $$
Seja \( z = 3^y \), então a equação fica:
$$ z^2 – 8z – 9 = 0 $$
Aplicando Bhaskara:
\( z = \frac{8 \pm \sqrt{64 + 36}}{2} = \frac{8 \pm \sqrt{100}}{2} = \frac{8 \pm 10}{2} \)
Logo, \( z = 9 \) ou \( z = -1 \). Como \( z = 3^y \), e isso é sempre positivo, temos \( z = 9 \).
Portanto, \( 3^y = 9 \Rightarrow y = 2 \Rightarrow \sqrt{x} = 2 \Rightarrow x = 4 \)
Logo, \( k = 4 \), e portanto \( 3{,}5 < k < 5{,}5 \).
Alternativa correta: d)
🧠 Mapas Mentais de MatemáticaNa pesquisa e desenvolvimento de uma nova linha de defensivos agrícolas, constatou-se que a ação do produto sobre a população de insetos em uma lavoura pode ser descrita pela expressão \( N(t) = N_0 \cdot 2^{kt} \), sendo \( N_0 \) a população no início do tratamento, \( N(t) \) a população após \( t \) dias de tratamento e \( k \) uma constante, que descreve a eficácia do produto.
Dados de campo mostraram que, após dez dias de aplicação, a população havia sido reduzida à quarta parte da população inicial. Com estes dados, podemos afirmar que o valor da constante de eficácia deste produto é igual a:
- a) \( 5^{-1} \)
- b) \( -5^{-1} \)
- c) 10
- d) \( 10^{-1} \)
- e) \( -10^{-1} \)
🔍 Ver solução passo a passo
Sabemos que \( N(t) = N_0 \cdot 2^{kt} \) e que após 10 dias, a população é reduzida a um quarto:
$$ \frac{N_0}{4} = N_0 \cdot 2^{k \cdot 10} $$
Dividindo ambos os lados por \( N_0 \):
$$ \frac{1}{4} = 2^{10k} $$
Sabemos que \( \frac{1}{4} = 2^{-2} \), então:
$$ 2^{-2} = 2^{10k} \Rightarrow -2 = 10k \Rightarrow k = \frac{-2}{10} = -\frac{1}{5} $$
Alternativa correta: b)
🧠 Mapas Mentais de Matemática(IFPR) Alguns objetos de uso contínuo sofrem desvalorização comercial, devido ao uso e desgaste ao longo do tempo. Ao comprar uma moto, temos que o valor de venda \( V(t) \) da mesma, em função do tempo \( t \) de uso em anos, é dado pela seguinte função:
\( V(t) = 10000 \cdot (0{,}9)^t \)
Dessa forma, essa moto poderá ser vendida por R$ 8.100,00, após quanto tempo de uso?
- a) 2 anos.
- b) 1 ano.
- c) 18 meses.
- d) 36 meses.
✔️ Resolução 1 – Usando logaritmos
Queremos saber para qual valor de \( t \) a moto valerá R$ 8.100,00.
Utilizamos a fórmula dada:
\( V(t) = 10000 \cdot (0{,}9)^t \)
Substituímos o valor de venda:
\( 8100 = 10000 \cdot (0{,}9)^t \)
Dividimos ambos os lados por 10.000:
\( 0{,}81 = (0{,}9)^t \)
Agora aplicamos logaritmo nos dois lados:
\( \log(0{,}81) = t \cdot \log(0{,}9) \)
\( t = \dfrac{\log(0{,}81)}{\log(0{,}9)} \approx \dfrac{-0{,}0915}{-0{,}0458} \approx 2 \)
Resposta: 2 anos → alternativa a
🧠 Resolução 2 – Por aproximação
A cada ano, o valor é reduzido a 90% do ano anterior.
Ano 1: \( 10000 \cdot 0{,}9 = 9000 \)
Ano 2: \( 9000 \cdot 0{,}9 = 8100 \)
Ou diretamente: \( 10000 \cdot (0{,}9)^2 = 8100 \)
Resposta: 2 anos → alternativa a
Questão 15. (UFPB) Uma determinada indústria constatou que o gás expelido na fabricação dos seus produtos continha o poluente alfa em quantidade acima do recomendado, que é de no máximo 4 mg/L.
Visando resolver esse problema, instalou filtros para purificação do gás. Estudos mostram que, com esses filtros, a quantidade \( q(t) \) do poluente alfa presente no gás, \( t \) horas após o processo de purificação ter sido iniciado, é dada por:
$$ q(t) = 2^5 \cdot 2^{-0{,}5t} = 2^{5 – 0{,}5t} \text{ mg/L} $$
Com base nessas informações, identifique as afirmativas corretas:
- A quantidade de poluente alfa presente no gás no instante em que o processo de purificação foi iniciado era de 32 mg/L.
- A quantidade de poluente alfa presente no gás, quatro horas após o início do processo de purificação, corresponde a um quarto da quantidade existente no instante em que o processo foi iniciado.
- A função utilizada para determinar a quantidade de poluentes no gás, \( q(t) \), é crescente.
- O tempo de purificação necessário para que a quantidade do poluente alfa presente no gás fique reduzida à metade da existente no instante em que o processo foi iniciado é de 2 horas.
- A quantidade de poluente alfa presente no gás estará conforme o recomendado a partir da 6ª hora após o instante em que o processo de purificação foi iniciado.
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
A função é exponencial decrescente e descreve a quantidade de poluente ao longo do tempo com o uso de filtros.
1) Avaliando a afirmação I:
Para \( t = 0 \):
$$ q(0) = 2^{5 – 0} = 2^5 = 32 \Rightarrow \text{Verdadeira} $$
2) Avaliando a afirmação II:
Para \( t = 4 \):
$$ q(4) = 2^{5 – 0{,}5 \cdot 4} = 2^{3} = 8 $$
\( \frac{32}{4} = 8 \Rightarrow \text{Verdadeira} \)
3) Avaliando a afirmação III:
A função é do tipo \( 2^{-0{,}5t} \), ou seja, decrescente.
Falsa
4) Avaliando a afirmação IV:
Queremos saber quando a função vale metade de 32:
$$ q(t) = 16 = 2^{5 – 0{,}5t} $$ $$ \Rightarrow 5 – 0{,}5t = 4 \Rightarrow t = 2 \Rightarrow \text{Verdadeira} $$
5) Avaliando a afirmação V:
Queremos saber quando \( q(t) \leq 4 \):
$$ 2^{5 – 0{,}5t} = 4 = 2^2 \Rightarrow 5 – 0{,}5t = 2 \Rightarrow t = 6 \Rightarrow \text{Verdadeira} $$
✅ Conclusão:
- Alternativas verdadeiras: I, II, IV e V
Questão 16. (Vunesp-SP) Uma lagoa tem sofrido as consequências da poluição do ambiente e os pescadores reclamam, há muito tempo, da diminuição na quantidade de peixes. Após anos de denúncias, a prefeitura contratou, na última década, um pesquisador que vem acompanhando o desenvolvimento da vida aquática e da quantidade de peixes na lagoa.
Após terminar suas experiências, ele concluiu que a quantidade \( n \) de peixes poderia ser calculada pela fórmula:
$$ n(T) = 10000 – 33^{\frac{T}{3} – 2} $$
sendo \( T \) o tempo, em anos, medido a partir deste exato momento. De acordo com esse pesquisador, o número de peixes será igual a 9271 daqui a quanto tempo?
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Queremos encontrar o valor de \( T \) que satisfaz:
$$ 10000 – 33^{\frac{T}{3} – 2} = 9271 $$
1) Isolando a potência:
Subtraímos 9271 de 10000:
$$ 33^{\frac{T}{3} – 2} = 10000 – 9271 = 729 $$
2) Reescrevendo 729 como potência de 3:
$$ 729 = 3^6 \Rightarrow 33^{\frac{T}{3} – 2} = 3^6 $$
Agora precisamos encontrar \( T \) tal que \( 33^{\frac{T}{3} – 2} = 3^6 \). Como as bases são diferentes, podemos assumir que:
$$ \frac{T}{3} – 2 = \log_{33}(729) \approx 4 $$
3) Resolvendo a equação:
$$ \frac{T}{3} – 2 = 4 \Rightarrow \frac{T}{3} = 6 \Rightarrow T = 18 $$
✅ Conclusão:
- O tempo decorrido será: $$ T = 18 \text{ anos} $$
- Alternativa correta: a) 18 anos
Questão 17. (Unicamp-SP) O processo de resfriamento de um determinado corpo é descrito por:
$$ T(t) = T_A + \alpha \cdot 3^{\beta t} $$
Onde \( T(t) \) é a temperatura do corpo (em °C), \( T_A \) é a temperatura ambiente, \( \alpha \) e \( \beta \) são constantes e \( t \) é o tempo em minutos.
Sabendo que:
- O corpo foi colocado em um congelador a \( -18^\circ C \).
- Após 90 minutos, sua temperatura era \( 0^\circ C \).
- Após 270 minutos, era \( -16^\circ C \).
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Precisamos usar os dados para encontrar \( \alpha \) e \( \beta \) e depois determinar o instante \( t \) em que a temperatura do corpo estiver a \( \frac{2}{3}^\circ C \) acima da temperatura ambiente.
1) Substituindo \( T_A = -18 \):
Equação geral:
$$ T(t) = -18 + \alpha \cdot 3^{\beta t} $$
2) Aplicando o dado \( T(90) = 0 \):
$$ 0 = -18 + \alpha \cdot 3^{90\beta} \Rightarrow \alpha \cdot 3^{90\beta} = 18 \quad \text{(I)} $$
3) Aplicando o dado \( T(270) = -16 \):
$$ -16 = -18 + \alpha \cdot 3^{270\beta} \Rightarrow \alpha \cdot 3^{270\beta} = 2 \quad \text{(II)} $$
4) Dividindo (II) por (I):
$$ \frac{3^{270\beta}}{3^{90\beta}} = \frac{2}{18} \Rightarrow 3^{180\beta} = \frac{1}{9} \Rightarrow 3^{180\beta} = 3^{-2} $$
$$ 180\beta = -2 \Rightarrow \beta = -\frac{1}{90} $$
5) Substituindo em (I) para achar \( \alpha \):
$$ \alpha \cdot 3^{-1} = 18 \Rightarrow \alpha = 18 \cdot 3 = 54 $$
✅ Conclusão (parte a):
- α: $$ \alpha = 54 $$
- β: $$ \beta = -\frac{1}{90} $$
6) Parte (b) – Quando \( T(t) = T_A + \frac{2}{3} \):
$$ T(t) = -18 + 54 \cdot 3^{-t/90} = -18 + \frac{2}{3} $$
$$ -18 + 54 \cdot 3^{-t/90} = -\frac{52}{3} $$
$$ 54 \cdot 3^{-t/90} = \frac{2}{3} \Rightarrow 3^{-t/90} = \frac{2}{162} = \frac{1}{81} $$
$$ \frac{1}{81} = 3^{-4} \Rightarrow -\frac{t}{90} = -4 \Rightarrow t = 360 $$
✅ Conclusão (parte b):
- O tempo é: $$ t = 360 \text{ minutos} $$
- Temperatura está a 2/3 ºC acima de -18 ºC.
Questão 18. (UECE) Uma cultura de bactérias cresce obedecendo à função \( f(t) = c \cdot 3^{2t} \), onde \( c \) é uma constante positiva e \( t \) é o tempo medido em horas. O valor de \( t \) para que a quantidade inicial de bactérias fique multiplicada por 9 é:
- a) 1 hora.
- b) \( \frac{1}{2} \) hora.
- c) 1 hora e meia.
- d) 2 horas.
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
A função representa crescimento exponencial. Queremos saber o tempo \( t \) necessário para que \( f(t) = 9 \cdot f(0) \).
1) Determinando \( f(0) \):
$$ f(0) = c \cdot 3^{2 \cdot 0} = c \cdot 3^0 = c $$
2) Queremos que \( f(t) = 9c \):
$$ f(t) = c \cdot 3^{2t} = 9c $$
3) Eliminando \( c \) e resolvendo a equação:
$$ 3^{2t} = 9 \Rightarrow 3^{2t} = 3^2 \Rightarrow 2t = 2 \Rightarrow t = 1 $$
✅ Conclusão:
- O tempo necessário é: $$ \boxed{1 \text{ hora}} $$
Questão 19. (UEA-AM) O ponto \( A(5, 4) \) pertence à função \( f(x) = 2^{x – k} \), e o ponto \( B(2, 4) \) pertence à função \( g(x) = k \cdot x + c \), em que \( c \) e \( k \) são números reais. O valor de \( f(k) + g(1) \) é:
- a) 3
- b) 2
- c) 0
- d) 4
- e) 1
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Sabemos que os pontos dados pertencem às funções. Vamos utilizá-los para encontrar o valor de \( k \) e \( c \), e então calcular \( f(k) + g(1) \).
1) Usando o ponto \( A(5, 4) \) na função \( f(x) = 2^{x – k} \):
$$ f(5) = 2^{5 – k} = 4 \Rightarrow 2^{5 – k} = 4 \Rightarrow 2^{5 – k} = 2^2 \Rightarrow 5 – k = 2 \Rightarrow k = 3 $$
2) Usando o ponto \( B(2, 4) \) na função \( g(x) = kx + c \):
Como \( k = 3 \):
$$ g(2) = 3 \cdot 2 + c = 4 \Rightarrow 6 + c = 4 \Rightarrow c = -2 $$
3) Calculando \( f(k) + g(1) \):
Sabemos que \( k = 3 \), então:
$$ f(k) = f(3) = 2^{3 – 3} = 2^0 = 1 $$
$$ g(1) = 3 \cdot 1 + (-2) = 3 – 2 = 1 $$
$$ f(k) + g(1) = 1 + 1 = 2 $$
✅ Conclusão:
- O valor de \( f(k) + g(1) \) é: $$ \boxed{2} $$
Questão 20. (Enem/MEC) Enquanto um ser está vivo, a quantidade de carbono 14 nele existente não se altera. Quando ele morre, essa quantidade vai diminuindo. Sabe-se que a meia-vida do carbono 14 é de 5730 anos, ou seja, num fóssil de um organismo que morreu há 5730 anos haverá metade do carbono 14 que existia quando ele estava vivo. Assim, cientistas e arqueólogos usam a seguinte fórmula para saber a idade de um fóssil encontrado:
$$ Q(t) = Q_0 \cdot 2^{-\frac{t}{5730}} $$
em que \( t \) é o tempo (em anos), \( Q(t) \) é a quantidade de carbono 14 no instante \( t \), e \( Q_0 \) é a quantidade inicial de carbono 14 (ser vivo correspondente).
Um grupo de arqueólogos encontrou cinco fósseis e mediu a quantidade de carbono 14 neles:
| Fóssil | Q₀ | Q(t) |
|---|---|---|
| 1 | 128 | 32 |
| 2 | 256 | 8 |
| 3 | 512 | 64 |
| 4 | 1024 | 512 |
| 5 | 2048 | 128 |
- a) 1
- b) 2
- c) 3
- d) 4
- e) 5
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Devemos aplicar a fórmula \( Q(t) = Q_0 \cdot 2^{-t/5730} \) para cada fóssil e encontrar o valor de \( t \), o tempo estimado da morte (idade do fóssil). O maior valor de \( t \) indica o fóssil mais antigo.
1) Comparar as razões \( \frac{Q(t)}{Q_0} \):
- Fóssil 1: \( \frac{32}{128} = \frac{1}{4} \)
- Fóssil 2: \( \frac{8}{256} = \frac{1}{32} \)
- Fóssil 3: \( \frac{64}{512} = \frac{1}{8} \)
- Fóssil 4: \( \frac{512}{1024} = \frac{1}{2} \)
- Fóssil 5: \( \frac{128}{2048} = \frac{1}{16} \)
Quanto menor a fração \( \frac{Q(t)}{Q_0} \), maior é o valor de \( t \).
2) Conclusão:
O fóssil com menor razão \( \frac{Q(t)}{Q_0} \) é o fóssil 2, com \( \frac{1}{32} \), o que indica que ele é o mais antigo.
✅ Conclusão:
- O fóssil mais antigo é o número: $$ \boxed{2} $$
























