Funções Trigonométricas: Seno e Cosseno
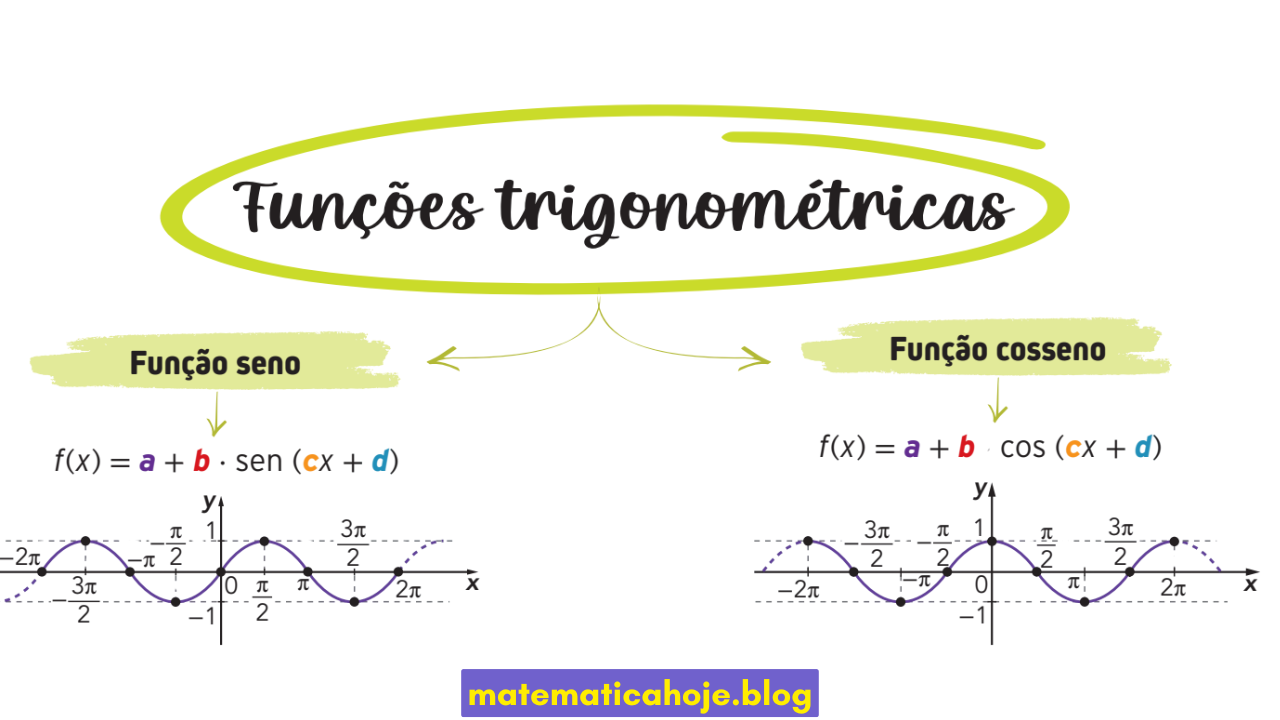
As funções trigonométricas são fundamentais no estudo da Matemática, especialmente em contextos que envolvem movimentos periódicos, ondas e cálculos geométricos. Entre elas, as mais conhecidas são a função seno e a função cosseno, que aparecem em uma grande variedade de aplicações práticas.
\( f(x) = a + b \cdot sen(cx + d) \)
\( f(x) = a + b \cdot \cos(cx + d) \)
Parâmetros e Transformações
- a: deslocamento vertical (translação em y);
- b: amplitude (altura da onda);
- c: frequência angular (quantas ondas cabem em \(2\pi\));
- d: deslocamento horizontal (fase).
Função Seno
A função seno na forma básica é \(f(x)=sen x\). Seu gráfico inicia em \(0\), atinge o valor máximo \(1\), depois o mínimo \(-1\), completando um ciclo em \(2\pi\).
Função Cosseno
A função cosseno na forma básica é \(f(x)=\cos x\). Diferente do seno, seu gráfico inicia em \(1\), também oscila entre \(1\) e \(-1\), repetindo-se a cada \(2\pi\).
Propriedades Importantes
- Ambas têm período \(2\pi\).
- \(sen x\) é ímpar (\(sen(-x)=-sen x\)).
- \(\cos x\) é par (\(\cos(-x)=\cos x\)).
- Imagem das duas funções: \([-1,1]\).
Exemplo Resolvido
Exemplo: Determine a amplitude, período e fase da função \(f(x)=2\cos(3x-\pi)\).
Solução:
• Amplitude = 2 (valor de \(b\));
• Período = \(\dfrac{2\pi}{3}\) (calculado como \(2\pi/c\));
• Fase = \(\pi/3\) (deslocamento horizontal).
Exercício de Múltipla Escolha
1) Qual é o período da função \(f(x)=sen(5x)\)?
A) \(2\pi\)
B) \(\pi\)
C) \(\dfrac{2\pi}{5}\)
D) \(\dfrac{\pi}{5}\)
Ver solução
O período é dado por \(\dfrac{2\pi}{c}=\dfrac{2\pi}{5}\). Resposta: C.






















