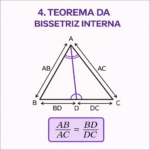
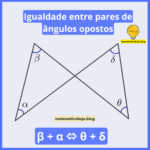
A Geometria Plana aparece em praticamente todas as provas que cobram matemática: ENEM, concursos, vestibulares e exames internos. Dominar áreas, perímetros, ângulos e propriedades das figuras planas é um passo decisivo para aumentar sua nota e ganhar confiança em questões visuais e de interpretação.
Geometria Plana estuda figuras que estão em um plano, como triângulos, quadrados, retângulos, círculos e outras formas que têm apenas duas dimensões: comprimento e largura. Os problemas mais comuns envolvem perímetro, área e relações entre ângulos.
Use os materiais do Matemática Hoje para transformar fórmulas soltas em um mapa claro de estudos:
O que é Geometria Plana?
Geometria Plana é o ramo da matemática que estuda figuras que estão em um plano, ou seja, não têm espessura: são bidimensionais. Exemplos típicos:
- Segmentos de reta e ângulos;
- Triângulos e quadriláteros (quadrado, retângulo, losango, trapézio);
- Polígonos em geral (pentágono, hexágono, etc.);
- Circunferências e círculos.
Em provas, esses assuntos aparecem cobrando:
- Cálculo de perímetro (soma dos lados);
- Cálculo de área (medida da superfície interna da figura);
- Uso de fórmulas específicas para cada figura;
- Questões de contexto: terrenos, plantas de arquitetura, mapas, embalagens, etc.
Não tente decorar tudo de uma vez. Comece pelas figuras mais cobradas (retângulo, quadrado, triângulo, círculo) e vá ampliando para outras conforme se sentir seguro.
Elementos básicos da Geometria Plana
Ponto, reta, semirreta e segmento
- Ponto: representa uma posição no plano, não tem dimensão.
- Reta: conjunto infinito de pontos, sem início nem fim.
- Semirreta: tem um ponto de origem e se estende infinitamente em uma direção.
- Segmento de reta: parte de uma reta limitada por dois pontos, com comprimento bem definido.
Ângulos e sua classificação
Um ângulo é formado por duas semirretas que partem de um mesmo ponto (vértice).
- Ângulo agudo: menor que $90^\circ$;
- Ângulo reto: igual a $90^\circ$;
- Ângulo obtuso: maior que $90^\circ$ e menor que $180^\circ$;
- Ângulo raso: igual a $180^\circ$;
- Ângulo completo: igual a $360^\circ$.
Em muitos problemas, identificar rapidamente o tipo de ângulo é a chave para saber qual fórmula aplicar ou qual propriedade usar.
Polígonos: o “alfabeto” das figuras planas
Um polígono é uma figura plana fechada, formada por segmentos de reta. Cada segmento é um lado, e os pontos de encontro são os vértices.
Classificação básica dos polígonos
- Triângulos: 3 lados;
- Quadriláteros: 4 lados;
- Pentágonos: 5 lados;
- Hexágonos: 6 lados;
- E assim por diante…
Em concursos e no ENEM, o foco principal recai sobre triângulos, quadriláteros notáveis e circunferência/círculo.
Triângulos: propriedades e fórmulas importantes
Classificação quanto aos lados
- Equilátero: três lados iguais;
- Isósceles: dois lados iguais;
- Escaleno: três lados diferentes.
Classificação quanto aos ângulos
- Retângulo: possui um ângulo reto ($90^\circ$);
- Acutângulo: todos os ângulos agudos;
- Obtusângulo: possui um ângulo obtuso (maior que $90^\circ$).
Propriedades fundamentais
- A soma dos ângulos internos de qualquer triângulo é $180^\circ$;
- O maior lado está sempre oposto ao maior ângulo;
- Em um triângulo retângulo, vale o Teorema de Pitágoras: $a^2 = b^2 + c^2$ (onde $a$ é a hipotenusa).
Área do triângulo
A fórmula mais usada é:
$A = \dfrac{b \cdot h}{2}$
Onde $b$ é a base e $h$ é a altura relativa a essa base. Em provas, a altura pode ser explícita, ou precisa ser encontrada com Pitágoras ou com relações trigonométricas.
Quadriláteros notáveis
Quadriláteros são polígonos de 4 lados. Os mais cobrados são: quadrado, retângulo, paralelogramo, losango e trapézio.
Quadrado
- Quatro lados iguais;
- Quatro ângulos retos;
- Área: $A = l^2$;
- Perímetro: $P = 4l$.
Retângulo
- Lados opostos paralelos e iguais;
- Quatro ângulos retos;
- Área: $A = b \cdot h$;
- Perímetro: $P = 2(b + h)$.
Paralelogramo
- Lados opostos paralelos e iguais;
- Ângulos opostos iguais;
- Área: $A = b \cdot h$ (base vezes altura);
- Perímetro: soma dos quatro lados.
Losango
- Quatro lados iguais;
- Lados opostos paralelos;
- Área: $A = \dfrac{D \cdot d}{2}$, onde $D$ e $d$ são as diagonais;
- Perímetro: $P = 4l$.
Trapézio
- Possui apenas um par de lados opostos paralelos (as bases);
- Área: $A = \dfrac{(B + b) \cdot h}{2}$;
- Perímetro: soma de todos os lados.
Circunferência e círculo
A circunferência é o contorno (linha) e o círculo é a região interna. Se $r$ é o raio:
- Comprimento da circunferência: $C = 2 \pi r$;
- Área do círculo: $A = \pi r^2$.
Em muitos enunciados, o problema fala em “rodas”, “tampas redondas”, “tanques cilíndricos vistos de cima” ou “pizzas”. Em todos esses casos, a base plana é um círculo, e você terá de usar $C = 2\pi r$ ou $A = \pi r^2$.
Resumo das principais fórmulas de área e perímetro
| Figura | Perímetro | Área |
|---|---|---|
| Quadrado (lado $l$) | $P = 4l$ | $A = l^2$ |
| Retângulo (base $b$, altura $h$) | $P = 2(b+h)$ | $A = b \cdot h$ |
| Triângulo (base $b$, altura $h$) | Soma dos lados | $A = \dfrac{b \cdot h}{2}$ |
| Losango (diagonais $D$ e $d$) | $P = 4l$ | $A = \dfrac{D \cdot d}{2}$ |
| Paralelogramo | Soma dos lados | $A = b \cdot h$ |
| Trapézio | Soma dos lados | $A = \dfrac{(B + b) \cdot h}{2}$ |
| Círculo (raio $r$) | $C = 2 \pi r$ | $A = \pi r^2$ |
Veja materiais para revisar Geometria Plana com foco em concurso:
Como Geometria Plana cai em provas de concurso e ENEM
Em provas, a banca quase nunca pede apenas “calcule a área deste quadrado”. Normalmente, a questão vem contextualizada: planta de uma casa, lote de terreno, placa de trânsito, quadra esportiva, embalagem, logotipo, etc.
- Interpretação de imagem: ler medidas na figura, identificar o tipo de figura;
- Combinação de figuras: área total como soma ou diferença de áreas simples;
- Problemas com unidades: converter cm para m, m para km, etc.;
- Questões envolvendo custo: preço por metro quadrado de piso, tinta, grama, etc.
Ao ler o enunciado, sublinhe:
- Que figura(s) aparecem;
- Quais são as medidas dadas (lados, bases, raios, diagonais);
- O que exatamente está sendo pedido (área, perímetro, diferença de áreas, custo, etc.).
Exemplos resolvidos de Geometria Plana
A seguir, alguns exemplos no padrão de concursos, com resolução passo a passo.
Exemplo 1 – Perímetro de um retângulo
Um terreno tem formato retangular, com comprimento de $18\,\text{m}$ e largura de $12\,\text{m}$. Qual é o perímetro desse terreno?
Ver solução comentada
Passo 1: Identificar a fórmula do perímetro do retângulo.
Para um retângulo, $P = 2(b + h)$, onde $b$ é a base e $h$ é a altura (ou largura).
Passo 2: Substituir os valores dados.
Aqui, podemos tomar $b = 18$ e $h = 12$.
$P = 2(b + h) = 2(18 + 12)$
Passo 3: Efetuar as operações.
$P = 2 \cdot 30 = 60\,\text{m}$
Resposta: o perímetro do terreno é de 60 metros.
Exemplo 2 – Área de um triângulo
Um triângulo tem base de $10\,\text{cm}$ e altura de $7\,\text{cm}$. Calcule a área desse triângulo.
Ver solução comentada
Passo 1: Anotar a fórmula da área do triângulo.
$A = \dfrac{b \cdot h}{2}$
Passo 2: Substituir $b = 10$ e $h = 7$.
$A = \dfrac{10 \cdot 7}{2}$
Passo 3: Efetuar as operações.
$A = \dfrac{70}{2} = 35\,\text{cm}^2$
Resposta: a área do triângulo é de $35\,\text{cm}^2$.
Exemplo 3 – Área de um círculo em situação prática
Uma praça circular será coberta com grama. O raio da praça é de $8\,\text{m}$. Considerando $\pi \approx 3{,}14$, qual é a área aproximada que será coberta de grama?
Ver solução comentada
Passo 1: Identificar a fórmula da área do círculo.
$A = \pi r^2$
Passo 2: Substituir $r = 8$ e $\pi \approx 3{,}14$.
$A \approx 3{,}14 \cdot 8^2$
Passo 3: Calcular $8^2$.
$8^2 = 64$
Passo 4: Multiplicar por $3{,}14$.
$A \approx 3{,}14 \cdot 64 \approx 200{,}96\,\text{m}^2$
Resposta: a área é de aproximadamente $201\,\text{m}^2$ (arredondando).
Como revisar Geometria Plana com eficiência
- Monte um resumão visual com as fórmulas principais;
- Faça uma lista de exercícios que misturem várias figuras na mesma questão;
- Treine conversão de unidades (cm, m, km; cm², m², etc.);
- Reveja questões clássicas do ENEM e de bancas de concurso.
Uma boa estratégia é combinar mapas mentais com um banco de questões específico de Geometria Plana. Assim, você vê o resumo e, em seguida, aplica em questões reais de prova.
Organize seus estudos com os materiais indicados:
Dica: salve esta página nos favoritos e volte sempre que precisar relembrar alguma fórmula de Geometria Plana.