📌 Função \( f(x) = e^x \): Gráfico, Propriedades e Aplicações
A função exponencial de base \( e \) é uma das mais importantes da matemática. Ela aparece em fenômenos naturais, crescimento populacional, juros compostos, modelos estatísticos e até mesmo em equações diferenciais. Neste artigo, você vai aprender o que é a função \( f(x) = e^x \), como é seu gráfico, quais são suas propriedades e por que ela é tão relevante.
✳️ O que é a função \( f(x) = e^x \)?
A função \( f(x) = e^x \) é uma função exponencial onde a base é o número irracional:
\( e \approx 2{,}71828 \)
Essa função é definida como:
\( f: \mathbb{R} \rightarrow \mathbb{R}^*, \quad f(x) = e^x \)
Ela é crescente, contínua, diferenciável e está presente em inúmeras áreas da matemática pura e aplicada.
📈 Gráfico da função \( f(x) = e^x \)
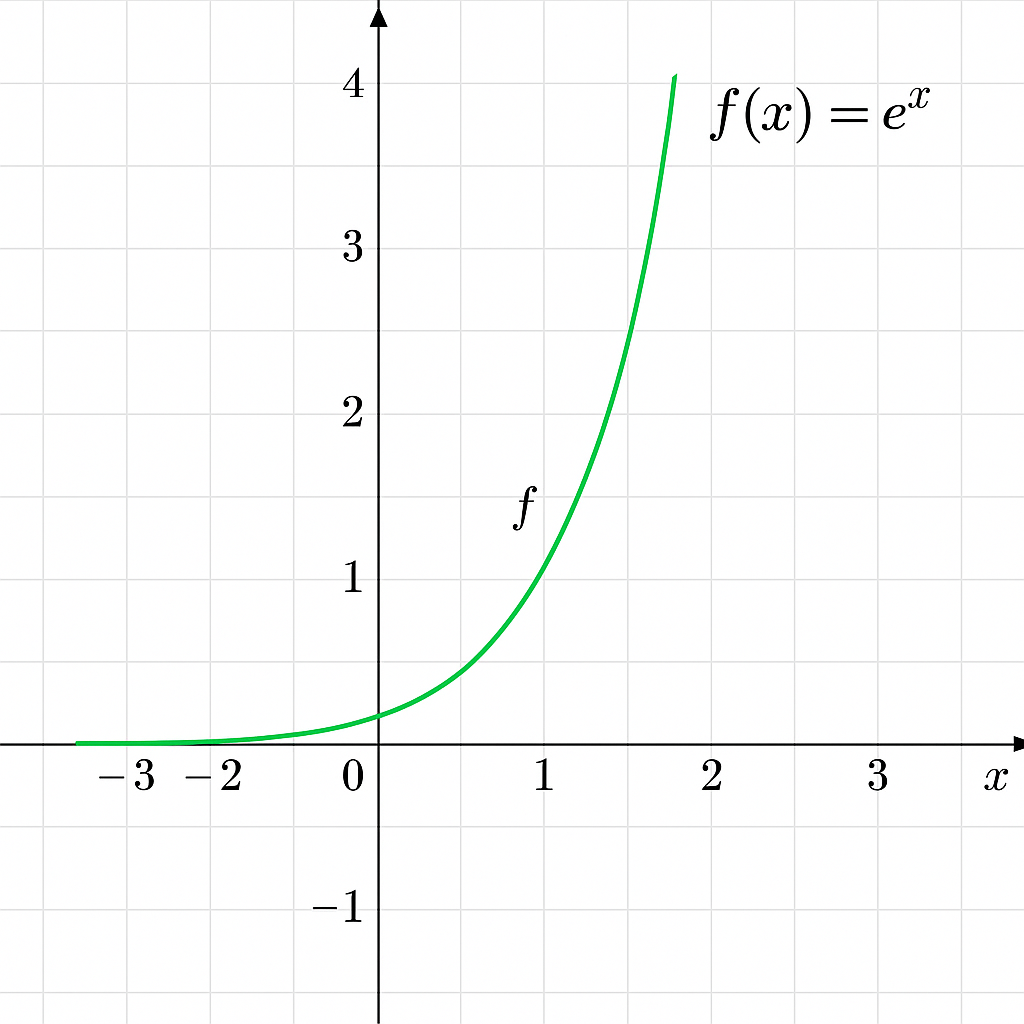
Figura – Gráfico da função \( f(x) = e^x \)
• O gráfico passa pelo ponto \( (0, 1) \)
• É sempre crescente
• O eixo x é uma assíntota horizontal
• Para \( x < 0 \), os valores se aproximam de 0, mas não se tornam negativos
🔍 Propriedades da função \( e^x \)
| Propriedade | Descrição |
|---|---|
| Domínio | \( \mathbb{R} \) |
| Imagem | \( \mathbb{R}^+ \) |
| f(0) | \( e^0 = 1 \) |
| Derivada | \( f'(x) = e^x \) |
| Comportamento | Crescente para todo \( x \) |
💡 Aplicações da função \( e^x \)
- Crescimento contínuo: população, bactérias, radioatividade
- Finanças: juros compostos contínuos
- Modelos físicos: resfriamento, circuitos elétricos
- Estatística: distribuições contínuas
- Equações diferenciais: solução natural de \( y’ = y \)
O número \( e \) é irracional e pode ser definido pelo limite:
\( e = \lim_{n \to \infty} \left(1 + \frac{1}{n} \right)^n \)
🤔 Pense e Responda
👉 Resposta: No ponto (0, 1)
• Qual o valor de \( f(1) \)?
👉 Resposta: \( f(1) = e \approx 2{,}718 \)
✅ Conclusão
A função \( f(x) = e^x \) é essencial para o estudo de crescimento exponencial contínuo. Seu gráfico mostra crescimento suave e constante, sua derivada é igual a ela mesma e sua presença na ciência é indiscutível. Dominar essa função é entender o coração da matemática moderna.
🧠 Baixar Mapa Mental da Função Exponencial





















