Conteúdo: Função afim – gráfico, coeficiente angular, lei da função e estudo do sinal.
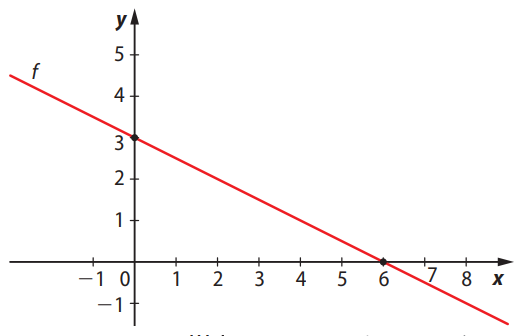
Enunciado: Observe o gráfico da função afim a seguir e faça o que se pede.
a) A função representada é crescente, decrescente ou constante? Justifique sua resposta. b) Determine a lei dessa função. c) Estude o sinal dessa função.🔍 Ver solução passo a passo
a) A função é crescente, decrescente ou constante?
Resposta: A função é decrescente, pois o gráfico é uma reta que desce da esquerda para a direita, indicando que o coeficiente angular é negativo.
b) Determine a lei dessa função.
Sabemos que a função é uma reta com intercepto em \( y = 3 \) e passa por \( (6, 0) \). Usamos a fórmula da reta:
Coeficiente angular:
\[ m = \frac{y_2 – y_1}{x_2 – x_1} = \frac{0 – 3}{6 – 0} = -\frac{1}{2} \]
Portanto, a função é: \[ f(x) = -\frac{1}{2}x + 3 \]
c) Estude o sinal dessa função.
- \( f(x) > 0 \) para \( x < 6 \)
- \( f(x) = 0 \) para \( x = 6 \)
- \( f(x) < 0 \) para \( x > 6 \)
✅ Conclusão:
Esta função afim apresenta uma taxa de variação negativa (coeficiente angular negativo), cruzando o eixo \( y \) em \( 3 \) e o eixo \( x \) em \( 6 \).
🧠 Mapas Mentais de Matemática