Gráfico de uma função do Primeiro Grau
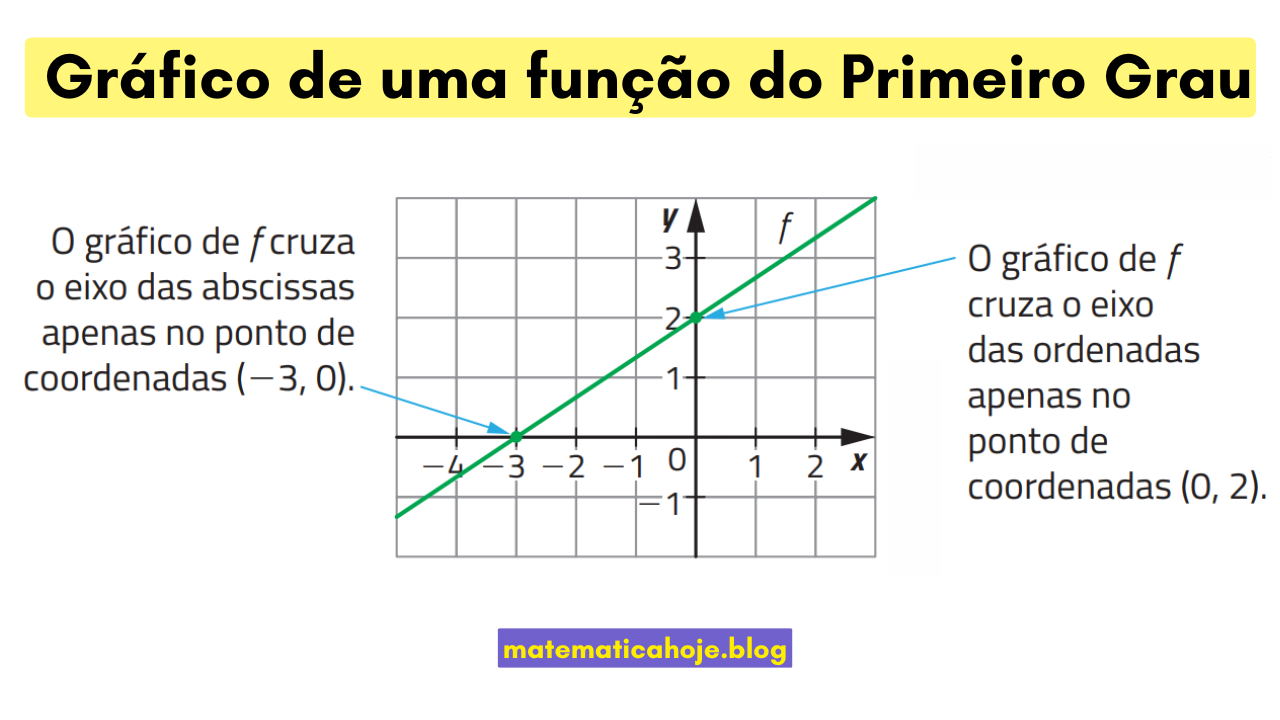
O gráfico de uma função do 1º grau \(f(x)=ax+b\) é sempre uma reta. Dois pontos definem completamente essa reta: o intercepto em \(y\) \(B=(0,b)\) e o zero (ou intercepto-x) \(x_0=-\dfrac{b}{a}\) (quando \(a\neq 0\)). A figura acima ilustra exatamente isso.
Componentes do gráfico
- Intercepto em \(y\): \(B=(0,b)\). É onde a reta corta o eixo vertical.
- Zero (intercepto-x): \(x_0=-\dfrac{b}{a}\). É onde a reta cruza o eixo \(x\) (veja detalhes).
- Inclinação (coeficiente angular): \(a=\dfrac{\Delta y}{\Delta x}\) (taxa de variação).
- Sinal de \(a\): se \(a\gt 0\) a reta sobe; se \(a\lt 0\) desce (estudo do sinal).
Passo a passo para desenhar \(f(x)=ax+b\)
- Marque no plano o ponto \(B=(0,b)\).
- Calcule o zero: \(x_0=-\dfrac{b}{a}\) (se \(a\neq 0\)) e marque \((x_0,0)\).
- Ligue os dois pontos com uma reta e prolongue nos dois sentidos.
- Opcional: confira a inclinação usando \(\dfrac{\Delta y}{\Delta x}=a\).
Se preferir outro método, você pode usar tabela de valores com dois \(x\) quaisquer e calcular \(f(x)\). Tutorial completo aqui: como construir o gráfico da função afim.
📘 Fórmulas na ponta da língua
Leve um resumo enxuto de funções (afim, linear, constante), gráficos e propriedades no eBook Fórmulas Matemática.
Baixar eBook de FórmulasExemplos resolvidos
Exemplo 1 — Interceptos e gráfico de \(f(x)=2x+2\).
a) Encontre \(B\) e \(x_0\). b) Esboce a reta e classifique (crescente/decrescente). c) Informe a inclinação.
Ver solução
a) \(B=(0,2)\). Zero: \(x_0=-\dfrac{2}{2}=-1\Rightarrow(-1,0)\).
b) \(a=2\gt 0\) ⇒ reta crescente. Ligue \((-1,0)\) a \((0,2)\).
c) Inclinação \(a=2=\dfrac{\Delta y}{\Delta x}\).
Exemplo 2 — Traçando via coeficiente angular.
Dada uma reta com \(a=-\dfrac{3}{2}\) e \(b=3\), construa o gráfico usando “sobe/desce”.
Ver solução
Marque \(B=(0,3)\). Como \(a=-\dfrac{3}{2}\), para cada avanço \(\Delta x=2\), descemos \(\Delta y=3\): ponto \((2,0)\). Una \((0,3)\) e \((2,0)\).
Exemplo 3 — Descobrindo a lei a partir do gráfico.
A reta passa por \(P(-3,0)\) e \(Q(0,2)\). Determine \(a\) e \(b\) e escreva \(f(x)\).
Ver solução
\(a=\dfrac{2-0}{0-(-3)}=\dfrac{2}{3}\). Como \(Q\) está no eixo \(y\), \(b=2\). Logo \(f(x)=\dfrac{2}{3}x+2\).
Exercícios propostos (com gabarito)
1) Para \(g(x)=-x+4\), determine \(B\), \(x_0\), a inclinação e classifique a reta. Em seguida, esboce o gráfico.
Gabarito
\(B=(0,4)\); \(x_0=-\dfrac{4}{-1}=4\Rightarrow(4,0)\); \(a=-1\lt 0\) ⇒ decrescente. Ligue \((0,4)\) e \((4,0)\).
2) Uma reta tem zero em \(x=5\) e passa por \(B=(0,-2)\). Encontre \(a\) e a lei \(f(x)\).
Gabarito
Dois pontos: \((5,0)\) e \((0,-2)\). \(a=\dfrac{0-(-2)}{5-0}=\dfrac{2}{5}\). Logo \(f(x)=\dfrac{2}{5}x-2\).
3) Em qual eixo a reta de \(h(x)=4x\) intercepta? Trace mentalmente o gráfico e justifique.
Gabarito
É função linear (\(b=0\)): passa pela origem. Intercepta ambos os eixos em \((0,0)\).
4) Dada \(p(x)=k x+1{,}5\), para que valores de \(k\) a reta é: a) crescente; b) decrescente; c) horizontal? Determine também o zero (quando existir).
Gabarito
a) Crescente: \(k\gt 0\), zero \(x_0=-1{,}5/k\). b) Decrescente: \(k\lt 0\), zero \(x_0=-1{,}5/k\). c) Horizontal: \(k=0\) ⇒ função constante \(f(x)=1{,}5\) (sem zero).
5) Esboce rapidamente a reta que passa por \(A(2,1)\) e tem inclinação \(a=3\). Indique um segundo ponto usando \(\Delta y/\Delta x\).
Gabarito
Com \(a=3=\dfrac{\Delta y}{\Delta x}\), para \(\Delta x=1\) sobe \(\Delta y=3\): ponto \(B(3,4)\). Trace a reta por \(A\) e \(B\).
Continue estudando Função Afim
- Como construir o gráfico da função afim
- Zero da função afim (raiz/intercepto-x)
- Taxa de variação da função afim (Δy/Δx)
- Estudo do sinal da função afim
- Interseção de retas
- Função linear (b=0) • Função constante (a=0)













