Gráfico de uma função inversa
Reflexão na reta \(y=x\), troca de eixos, inclinação de tangentes, exemplos e exercícios.
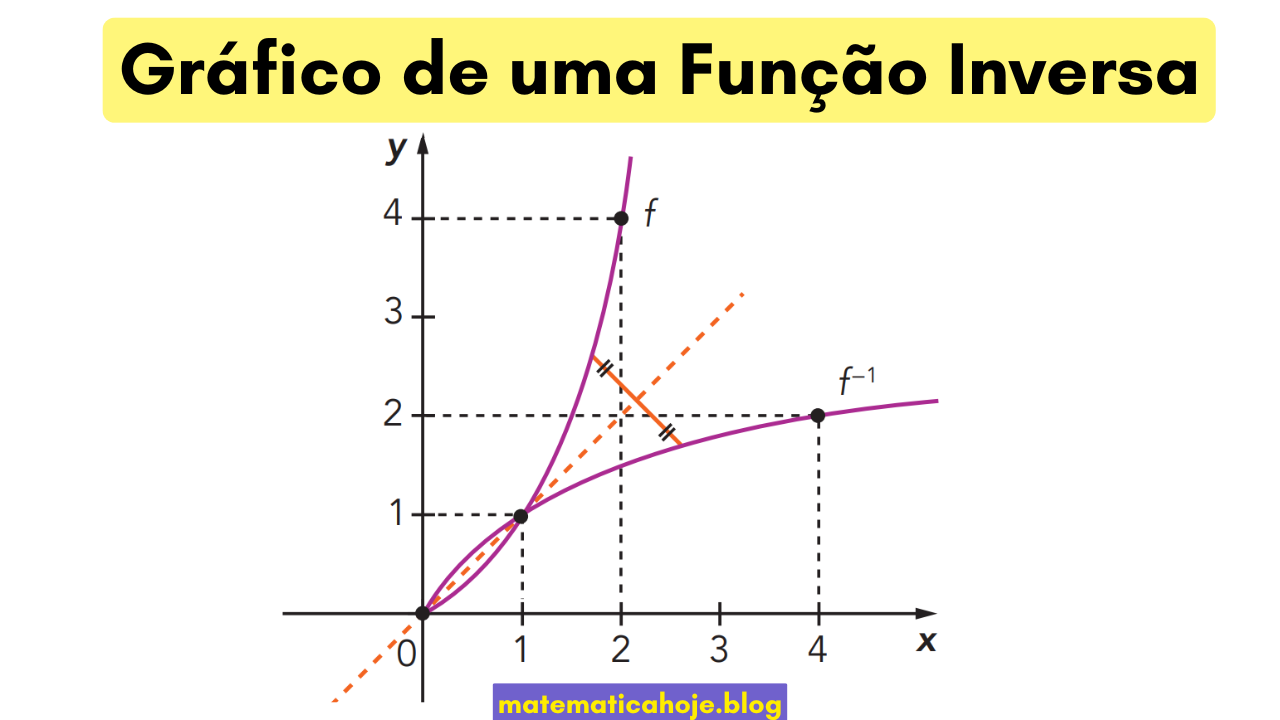
Se \(f:A\to B\) é bijetiva, sua inversa \(f^{-1}:B\to A\) “desfaz” \(f\). No plano cartesiano, o gráfico de \(f^{-1}\) é o gráfico de \(f\) refletido na reta \(y=x\).
Regras visuais essenciais
- Pares trocados: \((a,b)\in \text{graf}(f)\ \Longleftrightarrow\ (b,a)\in \text{graf}(f^{-1})\).
- Domínio e imagem trocam: \(D(f^{-1})=\operatorname{Im}(f)\) e \(\operatorname{Im}(f^{-1})=D(f)\).
- Interceptos trocam: se \(f(0)=k\), então o gráfico de \(f^{-1}\) passa por \((k,0)\). Se \(f(a)=0\), então \(f^{-1}\) passa por \((0,a)\).
- Assíntotas trocam: assíntota vertical \(x=a\) de \(f\) \(\Longleftrightarrow\) assíntota horizontal \(y=a\) de \(f^{-1}\) (e vice-versa).
- Monotonicidade: \(f\) crescente \(\Rightarrow\) \(f^{-1}\) crescente; \(f\) decrescente \(\Rightarrow\) \(f^{-1}\) decrescente.
Como desenhar \(f^{-1}\) a partir do gráfico de \(f\) (passo a passo)
- Trace a reta-guia \(y=x\) (45°).
- Marque alguns pontos fáceis em \(f\), como \((0,f(0))\), vértices, cruzamentos e pontos com coordenadas inteiras.
- Troque as coordenadas: \((x,y)\mapsto(y,x)\) e plote esses pontos.
- Conecte-os respeitando a forma (crescimento/descida) e assíntotas refletidas.
Exemplo da figura: se \(f(2)=4\), então \(f^{-1}(4)=2\). Se \(f(4)=2\), então \(f^{-1}(2)=4\). Note a simetria dos pontos em relação a \(y=x\).
Tabela-resumo
| Em \(f\) | Em \(f^{-1}\) | Observação |
|---|---|---|
| Ponto \((a,b)\) | Ponto \((b,a)\) | Pares trocados |
| Intercepto \(y=f(0)\) | Intercepto \(x=f(0)\) | Interceptos trocam |
| Assíntota vertical \(x=a\) | Assíntota horizontal \(y=a\) | “Vertical ↔ Horizontal” |
| Assíntota horizontal \(y=L\) | Assíntota vertical \(x=L\) | Idem |
| Derivada \(f'(x_0)\) | \((f^{-1})'(y_0)=1/f'(x_0)\) | \(y_0=f(x_0)\) |
| Crescente/Decrescente | Mesmo sentido | Preserva a ordem |
Exemplos rápidos
- \(f(x)=3x-6\): reta crescente que cruza \(y\) em \(-6\). A inversa é \(f^{-1}(x)=\dfrac{x+6}{3}\) (reta com inclinação \(1/3\)), obtida por reflexão.
- \(f(x)=e^x\): gráfico passa por \((0,1)\) e tem assíntota \(y=0\). A inversa \(\ln x\) passa por \((1,0)\) e tem assíntota \(x=0\).
- \(f(x)=x^2\) não é invertível em \(\mathbb{R}\) (falha no teste da reta horizontal). Restringindo a \(x\ge0\), o gráfico reflete em \(y=x\) para \(\sqrt{x}\).
Exercícios (múltipla escolha) com solução
1) O ponto \((2,5)\) pertence ao gráfico de \(f\). Qual ponto está, necessariamente, no gráfico de \(f^{-1}\)?
- \((5,5)\)
- \((5,2)\)
- \((2,2)\)
- \((\!-2,5)\)
Ver solução
2) Se o gráfico de \(f\) tem assíntota horizontal \(y=3\), então o gráfico de \(f^{-1}\) tem:
- assíntota horizontal \(y=3\)
- assíntota vertical \(x=3\)
- assíntota horizontal \(y=-3\)
- nenhuma assíntota
Ver solução
3) Dado \(f(2)=7\) e \(f'(2)=\dfrac{1}{5}\). Calcule \((f^{-1})'(7)\).
- \(5\)
- \(\dfrac{1}{5}\)
- \(-5\)
- \(0\)
Ver solução
4) O gráfico de \(f\) cruza o eixo \(x\) em \(x=4\). Qual afirmação é verdadeira sobre \(f^{-1}\)?
- cruza o eixo \(x\) em \(x=4\)
- cruza o eixo \(y\) em \(y=4\)
- tem assíntota \(x=4\)
- cruza o eixo \(y\) em \(y=-4\)
Ver solução
5) Em qual caso \(f^{-1}\) não é função (sem restringir o domínio)?
- \(f(x)=x^3-1\)
- \(f(x)=2x+1\)
- \(f(x)=e^x\)
- \(f(x)=x^2\)
Ver solução
Links internos (continue estudando)
• Funções inversas (definição e passos)
• Função bijetiva • Função injetiva • Função sobrejetiva
• Gráfico de uma Função • Domínio e Imagem • Plano Cartesiano
• Produtos do blog: Mapas Mentais • ENEM Matemática • Coleção 10 eBooks • Banco de Questões • eBook Fórmulas Matemática






















