Gráfico de uma Função Polinomial de 1º Grau

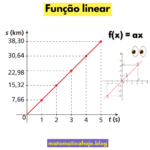
A função polinomial de 1º grau (ou função afim) é definida por $ f(x) = ax + b $ com $ a \ne 0 $. Seu gráfico é sempre uma reta. Tema recorrente no ENEM, vestibulares e concursos, dominar este conteúdo acelera sua evolução em mapas mentais e resolução de problemas.

Definição

$ f(x) = ax + b, \quad a \neq 0 $

a: coeficiente angular (inclinação da reta).
b: coeficiente linear (interseção com o eixo y).

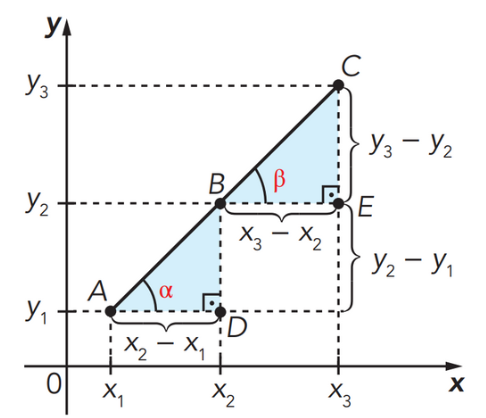
Demonstração: por que o gráfico é uma reta?

Se $A(x_1,y_1)$, $B(x_2,y_2)$ e $C(x_3,y_3)$ pertencem ao gráfico, então:

$\begin{aligned} y_1 &= ax_1 + b \quad \text{(I)}\\ y_2 &= ax_2 + b \quad \text{(II)}\\ y_3 &= ax_3 + b \quad \text{(III)} \end{aligned}$

Subtraindo (II) de (I): $ y_2 – y_1 = a(x_2 – x_1) $ (IV).
Subtraindo (III) de (II): $ y_3 – y_2 = a(x_3 – x_2) $ (V).
Dividindo (V) por (IV):

$\dfrac{y_3 – y_2}{y_2 – y_1} = \dfrac{x_3 – x_2}{x_2 – x_1}$

Logo, $A$, $B$ e $C$ estão alinhados: o gráfico é uma reta.

Gráfico de uma função polinomial de 1º grau

Interpretação geométrica

A inclinação é dada por:

$ a = \dfrac{y_2 – y_1}{x_2 – x_1} $

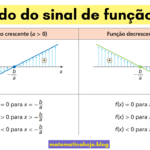
$a > 0$ → reta crescente;
$a < 0$ → reta decrescente;
$b$ é o ponto $ (0,b) $ no eixo y.

📘 Precisa das fórmulas sempre à mão?

Baixe o eBook Fórmulas Matemática com todas as principais fórmulas de funções, geometria, estatística e muito mais. Ideal para revisões rápidas e provas.

Baixar eBook de Fórmulas

Exemplo resolvido

Para $ f(x)=2x-4 $, encontre as interseções com os eixos e trace o gráfico.

Ver solução

No eixo y ($x=0$)

$ f(0)=2\cdot 0 -4=-4 \Rightarrow (0,-4) $

No eixo x ($f(x)=0$)

$ 2x-4=0 $

$ 2x=4 $

$ x=2 \Rightarrow (2,0) $

A reta é determinada pelos pontos $ (0,-4) $ e $ (2,0) $.

Exercícios propostos

1) Determine as interseções com os eixos de $ f(x)=-3x+6 $ e esboce o gráfico.

2) Um serviço cobra R$ 50,00 fixos + R$ 4,00 por hora. Modele por função e represente graficamente.

3) O gráfico de $ f(x)=ax+b $ passa por (1,2) e (3,6). Encontre $a$ e $b$.

Conclusão

O gráfico da função de 1º grau é uma reta cuja inclinação é definida por $a$ e a interseção com o eixo y por $b$. Este alicerce facilita o estudo de função quadrática e outros tópicos.

Links de produtos do blog

Relacionadas

Como Construir o Gráfico da Função Afim

Proporcionalidade direta e função linear

Coeficiente Angular

"Artigo escrito por"

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.