Gráfico de uma Função
Definição formal, leitura de informações no gráfico e técnicas para esboçar funções clássicas.
Antes de mergulhar nos gráficos, revise Plano Cartesiano, Ponto no Plano e a base de Domínio, Imagem e Contradomínio. Para treinar, use o Banco de Questões.
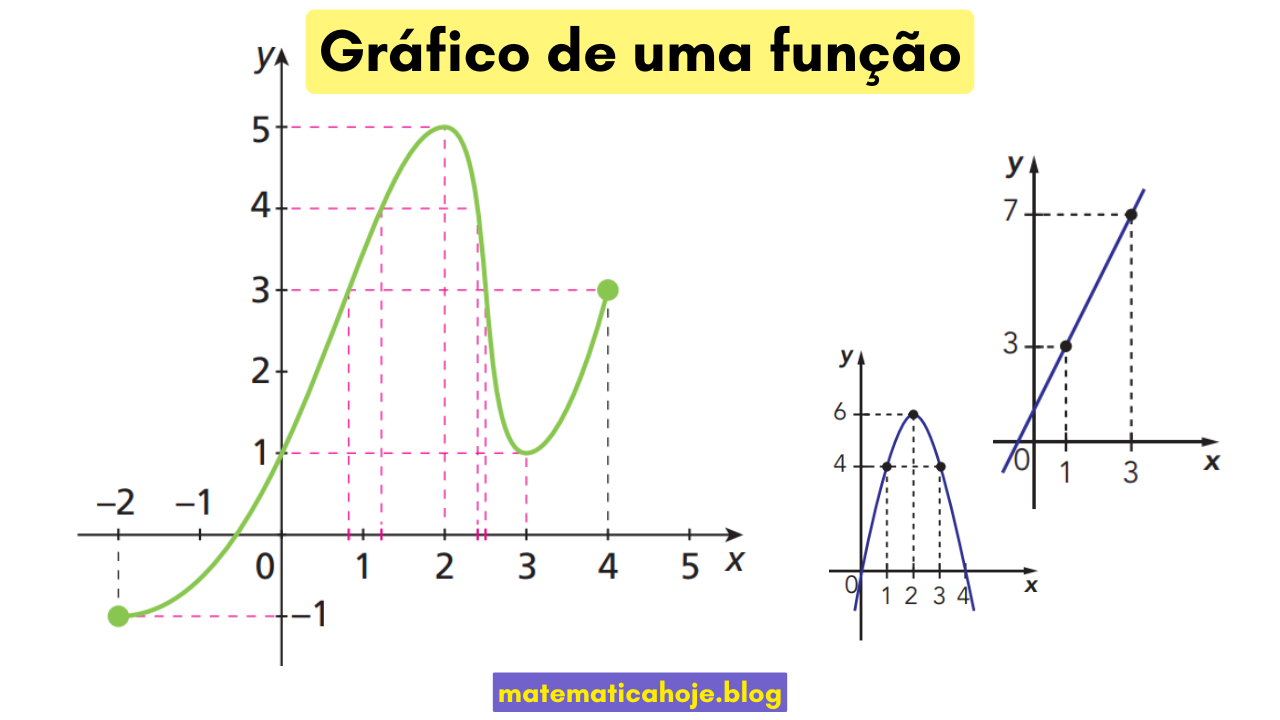
Leitura direta no gráfico
- Valor da função em \(x=a\): projete verticalmente até a curva e leia \(y=f(a)\).
- Zeros: abscissas onde a curva cruza o eixo \(x\) (soluções de \(f(x)=0\)).
- Intercepto em \(y\): ponto onde a curva cruza o eixo \(y\) (valor \(f(0)\)).
- Crescimento/decrescimento: em trechos ascendentes \(f\) cresce; descendentes, decresce.
- Máximo/Mínimo locais: picos e vales do gráfico; ajudam a descrever a imagem em intervalos.
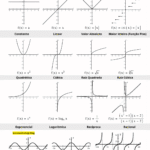
Famílias clássicas de gráficos
| Função | Forma do gráfico | Pontos-chave |
|---|---|---|
| Afim \(y=mx+b\) | Reta | Inclinação \(m\); intercepto \(b=f(0)\); zero em \(-b/m\) (se \(m\neq0\)) |
| Quadrática \(y=ax^2+bx+c\) | Parábola | Vértice \(\left(\!-\,\frac{b}{2a},\,\frac{-\Delta}{4a}\right)\); abre p/ cima se \(a>0\) |
| Módulo \(y=|x|\) ou \(y=|ax+b|\) | “V” | Quebra onde o argumento do módulo zera |
| Exponencial \(y=a^x\) \((a>1)\) | Crescente | Ponto \((0,1)\); nunca cruza \(y=0\) |
| Logarítmica \(y=\log_a x\) | Cresce devagar | Passa em \((1,0)\); domínio \(x>0\) |
Para aprofundar: Equações do 1º Grau, Função do 2º Grau, Logaritmos.
Transformações que “movem” o gráfico
- Translação vertical: \(y=f(x)+k\) move \(k\) unidades no eixo \(y\).
- Translação horizontal: \(y=f(x-h)\) move \(h\) unidades no eixo \(x\) (para a direita se \(h>0\)).
- Reflexões: \(y=-f(x)\) espelha no eixo \(x\); \(y=f(-x)\) espelha no eixo \(y\).
- Alongamentos: \(y=a\cdot f(x)\) estica/comprime verticalmente; \(y=f(bx)\) horizontalmente.
Exemplos comentados
1) Lendo valores no gráfico
Se o gráfico passa por \((1,3)\) e \((3,7)\), então \(f(1)=3\) e \(f(3)=7\). Se cruza o eixo \(x\) em \(x=2\), então \(f(2)=0\) (zero).
2) Esboço rápido — reta
\(f(x)=2x-1\). Intercepto: \(f(0)=-1\) → ponto \((0,-1)\). Zero: \(2x-1=0\Rightarrow x=\tfrac12\) → ponto \((\tfrac12,0)\). Trace a reta por esses dois pontos.
3) Esboço rápido — parábola
\(g(x)=x^2-4x+3\). \(\Delta=16-12=4\) → zeros: \(x=1\) e \(x=3\). Vértice: \(\left(2, -1\right)\). A parábola abre para cima e toca o eixo \(x\) em 1 e 3.
4) Função por partes
\(h(x)=\begin{cases}2x+1,&x\le 0\\ x^2,&x>0\end{cases}\). Esboce cada lei em seu intervalo; verifique continuidade em \(x=0\): \(h(0^-)=1\) e \(h(0^+)=0\) → salto.
Exercícios (múltipla escolha) com solução
1) A reta que passa por \((0,3)\) e \((2,7)\) tem equação:
- \(y=2x+3\)
- \(y=4x-1\)
- \(y=3x+1\)
- \(y=x+3\)
Ver solução
2) No gráfico da parábola \(y=-(x-2)^2+6\), o vértice é:
- \((2,6)\)
- \((6,2)\)
- \((0,6)\)
- \((2,-6)\)
Ver solução
3) A imagem de \(f(x)=|x|-2\) é:
- \([0,\infty)\)
- \((-\infty,2]\)
- \([-2,\infty)\)
- \((-\infty,-2]\)
Ver solução
4) O gráfico de \(y=f(x)\) cruza o eixo \(x\) em \(x=-1\) e \(x=3\) e o eixo \(y\) em \(y=3\). Qual das opções pode ser \(f(x)\)?
- \(f(x)=x^2-2x-3\)
- \(f(x)=x^2-3x-4\)
- \(f(x)=x^2+2x-3\)
- \(f(x)=x^2-2x+3\)
Ver solução
5) A transformação \(y=f(x-4)+2\) desloca o gráfico de \(f\):
- 4 à esquerda e 2 para cima
- 4 à direita e 2 para cima
- 4 à direita e 2 para baixo
- 4 à esquerda e 2 para baixo
Ver solução
6) Para a exponencial \(g(x)=3^x\), assinale a correta:
- Passa por \((0,3)\) e tem assíntota em \(x=0\)
- Passa por \((1,0)\) e tem assíntota em \(y=0\)
- Passa por \((0,1)\) e tem assíntota em \(y=0\)
- Passa por \((0,1)\) e cruza \(y=0\) em \(x=1\)
Ver solução
Continue estudando (links internos)
• Função do 2º Grau
• Equações do 1º Grau
• Ponto no Plano Cartesiano
• Roteiro ENEM Matemática
• Coleção 10 eBooks de Matemática