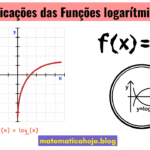
Imagem da Função Logarítmica
Veja também:
Função logarítmica (definição e gráfico) •
Propriedades da função logarítmica •
Mudança de base •
Logaritmo natural (ln)
Para base \(a>0\) e \(a\neq1\), a função logarítmica é \( f(x)=\log_a x \) com domínio \( (0,\infty) \). A pergunta aqui é: qual é a imagem?
\( \displaystyle \operatorname{Im}(f)=\mathbb{R} \)
O logaritmo pode assumir qualquer valor real: quando \(0
Por que a imagem é \(\mathbb{R}\)?
\( \lim_{x\to 0^+}\log_a x=-\infty \) (assíntota em \(x=0\))
\( \log_a 1=0 \Rightarrow (1,0) \) pertence ao gráfico
\( \lim_{x\to +\infty}\log_a x=+\infty \) se \(a>1\) (ou \(-\infty\) se \(0
Resumo rápido
- Domínio: \( (0,\infty) \)
- Imagem: \( \mathbb{R} \)
- Assíntota vertical: \( x=0 \)
- Ponto notável: \( (1,0) \)
- Crescimento: crescente se \(a>1\); decrescente se 0 < a < 1
Aplicações práticas
- Escalas logarítmicas (decibéis, Richter, pH);
- Crescimento e decaimento com mudanças de ordem de grandeza;
- Modelagem em dados que variam por múltiplos.
Exercícios rápidos
1) A imagem de \( f(x)=\log_5 x \) é:
- a) \( (0,\infty) \)
- b) \( \mathbb{R} \)
- c) \( [0,\infty) \)
- d) \( (-\infty,0] \)
Ver solução
\( \mathbb{R} \). Alternativa b.
2) Qual é o domínio de \( g(x)=\log_{1/2}(x-3) \)? E sua imagem?
Ver solução
Domínio: \( x-3>0 \Rightarrow x>3 \). Imagem: \( \mathbb{R} \) (independe da base, desde que \(a>0\) e \(a\neq1\)).
Leituras internas recomendadas (SEO)
- Função logarítmica — guia com gráfico
- Propriedades da função logarítmica
- Mudança de base do logaritmo
- Logaritmo natural (ln)
Materiais e produtos do blog
Relacionadas
