Inclinação da Reta (Coeficiente Angular) — Fórmulas, Exemplos e Exercícios
Neste guia você aprende, de forma direta e visual, como calcular a inclinação da reta — também chamada de coeficiente angular e representada por \(m\). Vamos relacionar \(m\) com o ângulo que a reta faz com o eixo \(X\), ver como obter \(m\) a partir de dois pontos ou da equação da reta, e praticar com exercícios comentados.
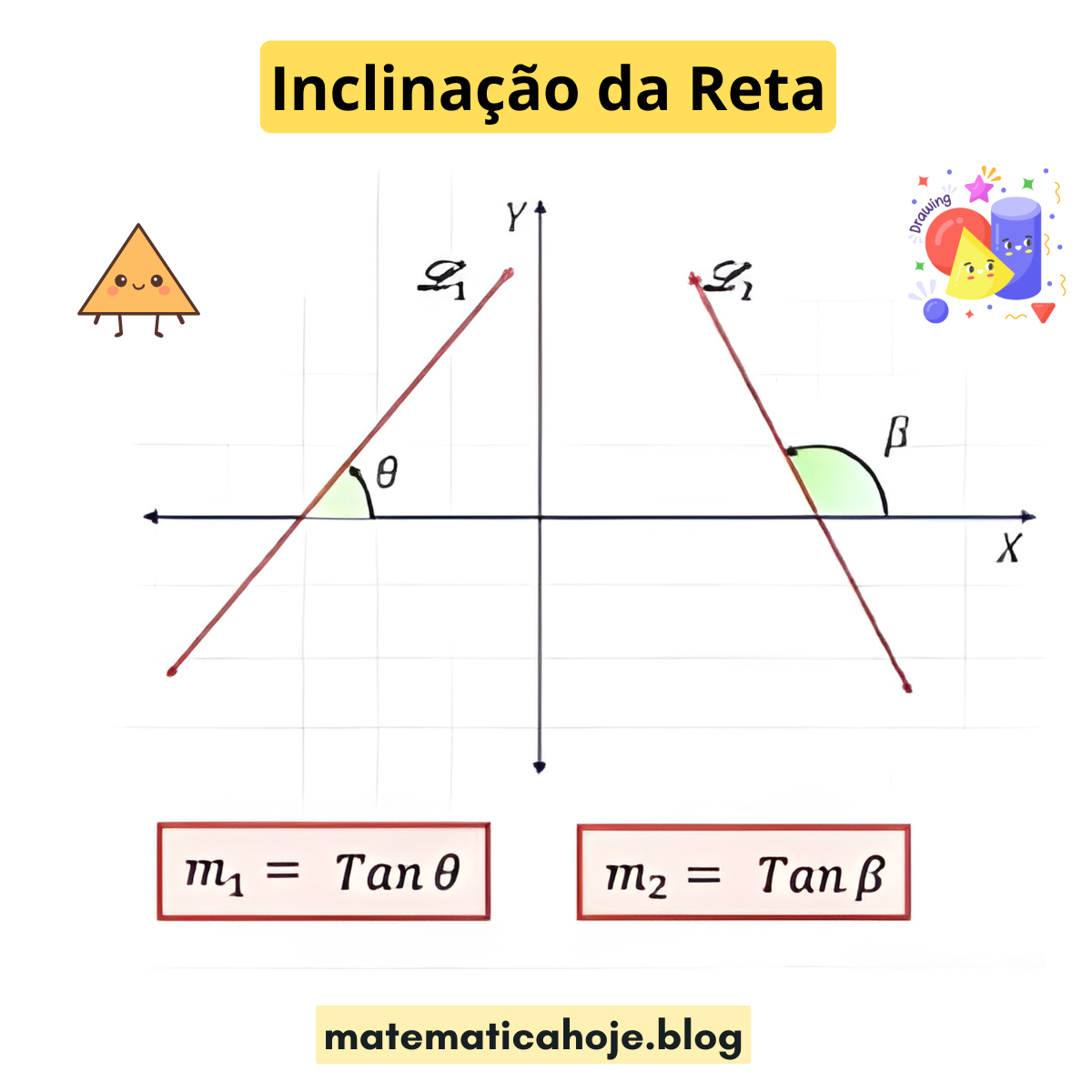
O que é a Inclinação (coeficiente angular)
Considere uma reta \( \ell \) no plano cartesiano. A inclinação mede o quanto a reta “sobe” (variação em \(y\)) para cada unidade que ela “anda” para a direita (variação em \(x\)).
Quando a reta faz um ângulo \( \theta \) com o eixo \(X\) (medido a partir do eixo \(X\) positivo, no sentido anti-horário), vale a relação trigonométrica:
Fórmulas essenciais
1) A partir de dois pontos \(A(x_1,y_1)\) e \(B(x_2,y_2)\):
2) A partir da equação explícita \(y = mx + b\):
3) A partir da forma geral \(ax + by + c = 0\) (com \(b \ne 0\)):
4) Paralelismo e perpendicularidade (retas não verticais):
eBook — Fórmulas Matemática (download gratuito)
Exemplos resolvidos
Exemplo 1 — Dois pontos. Encontre a inclinação da reta que passa por \(A(1,2)\) e \(B(5,10)\).
Solução:
\( m = \dfrac{y_2 – y_1}{x_2 – x_1} \)
\( m = \dfrac{10 – 2}{5 – 1} \)
\( m = \dfrac{8}{4} \)
\( m = 2 \)
Resposta: \(m = 2\).
Exemplo 2 — Forma geral. Determine \(m\) da reta \(3x – 2y + 6 = 0\).
Solução:
\( m = -\dfrac{a}{b} \) com \(a=3\) e \(b=-2\)
\( m = -\dfrac{3}{-2} \)
\( m = \dfrac{3}{2} \)
Resposta: \(m = \dfrac{3}{2}\).
Exemplo 3 — Ângulo de inclinação. Uma reta tem \(m = -\dfrac{1}{\sqrt{3}}\). Calcule o ângulo \( \theta \) com o eixo \(X\) (em graus).
Solução:
\( m = \tan\theta \)
\( -\dfrac{1}{\sqrt{3}} = \tan\theta \)
\( \theta = -30^\circ \) (ou \(150^\circ\), direções coterminais)
Resposta: Ângulo de inclinação pode ser tomado como \(150^\circ\) no intervalo \((0^\circ,180^\circ)\).
Lista de exercícios (com soluções)
1. Calcule a inclinação da reta que passa por \(A(-2,3)\) e \(B(4,-1)\).
\( m = \dfrac{-4}{6} \)
\( m = -\dfrac{2}{3} \)
2. Determine \(m\) da reta \(2x + 5y – 20 = 0\).
3. A reta \(r\) é paralela a \(y = -3x + 1\). Qual é a inclinação de \(r\)?
\( m_r = -3 \)
4. A reta \(s\) é perpendicular a \(y = \dfrac{1}{2}x – 4\). Encontre \(m_s\).
\( m_s = -2 \)
5. (Múltipla escolha) A inclinação da reta que passa por \(P(3, -2)\) e \(Q(9, 1)\) é:
- A) \( \dfrac{1}{3} \)
- B) \( \dfrac{1}{2} \)
- C) \( \dfrac{2}{3} \)
- D) \( \dfrac{3}{2} \)
\( m = \dfrac{3}{6} \)
\( m = \dfrac{1}{2} \) → ✅ Alternativa B
6. (Estilo ENEM) Uma rampa deve obedecer \(m = 0{,}08\). Para cada 5 metros na horizontal, a variação vertical será de:
\( \Delta y = 0{,}08 \cdot 5 \)
\( \Delta y = 0{,}40 \) metro
7. Encontre o ângulo de inclinação de \(y = \sqrt{3}\,x\) (em graus).
\( \theta = 60^\circ \)
8. (Desafio) A reta que passa por \(A(1,1)\) e \(B(k,5)\) tem inclinação \(m=2\). Encontre \(k\).
\( \dfrac{4}{k – 1} = 2 \)
\( 4 = 2(k – 1) \)
\( 4 = 2k – 2 \)
\( 6 = 2k \)
\( k = 3 \)













