Inequações do 1º grau: passo a passo completo
Resolver uma inequação do 1º grau é encontrar os valores de \(x\) que tornam verdadeira uma desigualdade do tipo \(ax+b\ \square\ 0\) (com \(\square\) sendo \(>\), \(\ge\), \(<\) ou \(\le\)). Você pode resolver por isolamento algébrico, estudo do sinal (usando o zero \(x_0=-\tfrac{b}{a}\)) ou pela leitura no gráfico de \(y=ax+b\). Antes, revise: crescente x decrescente, coeficiente angular e como traçar a reta.
1) Método algébrico (isolar o \(x\))
- Leve todos os termos com \(x\) para um lado e os números para o outro.
- Atenção: ao multiplicar ou dividir por número negativo, inverta o sentido da desigualdade.
- Escreva a solução em intervalos.
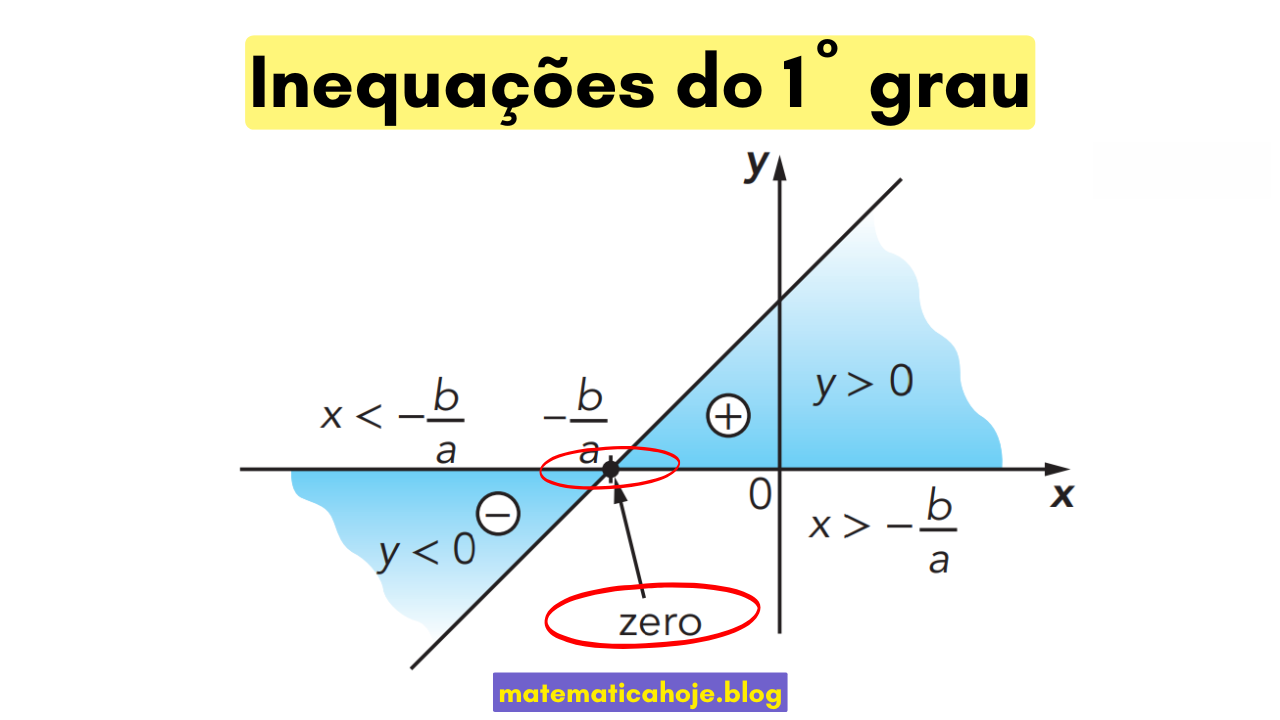
2) Método do zero e do sinal
Considere \(f(x)=ax+b\) com \(a\ne0\) e \(x_0=-\dfrac{b}{a}\).
- Se \(a\gt0\): \(f(x)\gt0\) para \(x\gt x_0\) e \(f(x)\lt0\) para \(x\lt x_0\).
- Se \(a\lt0\): inverta os sentidos.
- Para \(\ge\) ou \(\le\), inclua o ponto \(x_0\).
É exatamente a leitura do estudo do sinal para a função afim.
📘 Precisa revisar fórmulas rápidas?
Baixe o eBook Fórmulas Matemática com resumos de funções, inequações e trigonometria — perfeito para ENEM e vestibulares.
Baixar eBook de Fórmulas3) Método gráfico
Trace a reta \(y=ax+b\). As soluções de \(ax+b\ \square\ 0\) são as abscissas dos pontos onde:
- \(y\gt0\): parte acima do eixo \(x\);
- \(y\lt0\): parte abaixo do eixo \(x\);
- \(y\ge0\) ou \(\le0\): inclua o(s) ponto(s) onde a reta toca o eixo \(x\) (zero).
Veja gráfico do 1º grau e passo a passo para construir a reta.
Exemplos resolvidos
Exemplo 1 — Básico. Resolva \(2x-5>9\).
Ver solução
\(2x>14\Rightarrow x>7\). Intervalo: \((7,+\infty)\).
Exemplo 2 — Coeficiente negativo. Resolva \(-3x+6\ge0\).
Ver solução
\(-3x\ge-6\Rightarrow x\le2\) (inverte ao dividir por \(-3\)). Intervalo: \((-\infty,2]\).
Exemplo 3 — Ambos os lados com \(x\). Resolva \(2x+3<5x-9\).
Ver solução
Traga \(x\) à direita e números à esquerda: \(12<3x\Rightarrow x>4\). Intervalo: \((4,+\infty)\).
Exemplo 4 — Frações com denominador positivo. Resolva \(\dfrac{2x-1}{3}\le5\).
Ver solução
Multiplicar por \(3>0\) não muda o sinal: \(2x-1\le15\Rightarrow 2x\le16\Rightarrow x\le8\). Intervalo: \((-\infty,8]\).
Exemplo 5 — Inequação dupla (conjunção). Resolva \(1\ \le\ 2x-3\ \lt\ 5\).
Ver solução
Quebre em duas: \(1\le2x-3\Rightarrow x\ge2\) e \(2x-3<5\Rightarrow x<4\). Interseção: \([2,4)\).
Exemplo 6 — Valor absoluto (reduz a duas inequações de 1º grau). Resolva \(|2x-3|\le5\).
Ver solução
\(-5\le2x-3\le5\Rightarrow -2\le2x\le8\Rightarrow -1\le x \le4\). Intervalo: \([-1,4]\).
Erros comuns (e como evitar)
- Esquecer de inverter a desigualdade ao dividir por número negativo.
- Trocar união por interseção: inequação dupla usa interseção; sistema com “ou” usa união.
- Perder o ponto de igualdade em \(≥\) ou \(≤\): inclua a “bolinha fechada”/colchete no intervalo.
Exercícios propostos (com gabarito)
1) Resolva \(5-2x\ge -1\).
Gabarito
\(-2x\ge -6 \Rightarrow x\le 3\). \((-\infty,3]\).
2) Resolva \(\dfrac{x+4}{2}\gt \dfrac{3x-2}{4}\).
Gabarito
Multiplique por \(4>0\): \(2(x+4)>(3x-2)\Rightarrow 2x+8>3x-2\Rightarrow 10>x\Rightarrow x<10\). \((-\infty,10)\).
3) Encontre a solução de \(a x+b\le0\) supondo \(a\gt0\).
Gabarito
\(x\le -\dfrac{b}{a}\). Se \(a\lt0\), seria \(x\ge -\dfrac{b}{a}\). Relacione com o estudo do sinal.
4) Resolva o sistema \(\begin{cases}x-2\ge0\\ 3x+1<10\end{cases}\).
Gabarito
Primeira: \(x\ge2\). Segunda: \(3x<9\Rightarrow x<3\). Interseção: \([2,3)\).
5) Resolva \(|x-5|>3\) (escreva em união de intervalos).
Gabarito
\(x-5>3\) ou \(x-5<-3\Rightarrow x>8\) ou \(x<2\). Intervalo: \((-\infty,2)\cup(8,\infty)\).













