ITA 2024 — 2ª Fase — Questão 06 — Geometria Espacial
O sólido \(S\) é formado pela união de dois paralelepípedos retângulos congruentes, com posição e medidas conforme a figura.
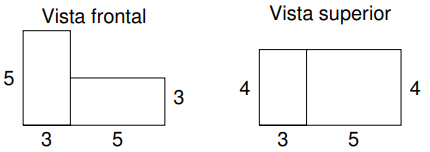
Seja \(AB\) um segmento de reta completamente contido em \(S\) que contém um dos vértices de \(S\).
Encontre o maior valor possível de \(m(AB)\).
👀 Solução passo a passo
I) Semelhança dos triângulos CDF e CEA:
\[ \frac{DF}{4} = \frac{3}{8} \quad \Rightarrow \quad DF = \frac{3}{2} \] II) Cálculo de FG:
\[ FG = DG – DF = 4 – \frac{3}{2} = \frac{5}{2} \] III) Teorema de Pitágoras:
a) No triângulo CEA: \[ (CA)^2 = (CE)^2 + (EA)^2 = 8^2 + 4^2 \Rightarrow CA = \sqrt{80} \] b) No triângulo AGF: \[ (FA)^2 = (FG)^2 + (GA)^2 = \left(\frac{5}{2}\right)^2 + 5^2 = \frac{125}{4} \] IV) Semelhança dos triângulos BCA e EFA:
\[ \frac{BC}{HF} = \frac{CA}{FA} \quad \Rightarrow \quad BC = \frac{\sqrt{80}}{\frac{\sqrt{125}}{2}} \cdot 3 = \frac{24}{5} \] V) Teorema de Pitágoras no triângulo BCA:
\[ (AB)^2 = (BC)^2 + (CA)^2 = \left(\frac{24}{5}\right)^2 + 80 = \frac{2576}{25} \] \[ AB = \frac{4\sqrt{161}}{5} \]
\[ \frac{DF}{4} = \frac{3}{8} \quad \Rightarrow \quad DF = \frac{3}{2} \] II) Cálculo de FG:
\[ FG = DG – DF = 4 – \frac{3}{2} = \frac{5}{2} \] III) Teorema de Pitágoras:
a) No triângulo CEA: \[ (CA)^2 = (CE)^2 + (EA)^2 = 8^2 + 4^2 \Rightarrow CA = \sqrt{80} \] b) No triângulo AGF: \[ (FA)^2 = (FG)^2 + (GA)^2 = \left(\frac{5}{2}\right)^2 + 5^2 = \frac{125}{4} \] IV) Semelhança dos triângulos BCA e EFA:
\[ \frac{BC}{HF} = \frac{CA}{FA} \quad \Rightarrow \quad BC = \frac{\sqrt{80}}{\frac{\sqrt{125}}{2}} \cdot 3 = \frac{24}{5} \] V) Teorema de Pitágoras no triângulo BCA:
\[ (AB)^2 = (BC)^2 + (CA)^2 = \left(\frac{24}{5}\right)^2 + 80 = \frac{2576}{25} \] \[ AB = \frac{4\sqrt{161}}{5} \]
Resposta: \( \frac{4\sqrt{161}}{5} \)






















