Questão 48 – Interpretação de Intervalos na Reta Real
Enunciado:
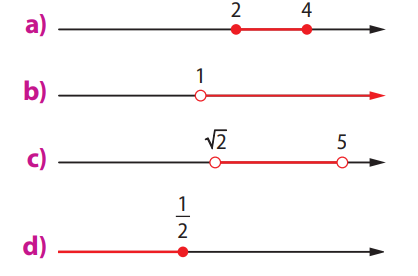
Usando a notação de conjuntos, escreva os intervalos a seguir, que estão representados na reta real:
Ver Solução
a) Os pontos 2 e 4 estão preenchidos (fechados), indicando que eles pertencem ao intervalo.
\( \{x \in \mathbb{R} \mid 2 \leq x \leq 4\} \)
b) A partir de 1, com círculo aberto, indo para a direita: intervalo aberto em 1 e sem limite superior.
\( \{x \in \mathbb{R} \mid x > 1\} \)
c) Intervalo aberto de \( \sqrt{2} \) até 5 (ambos com círculos abertos).
\( \{x \in \mathbb{R} \mid \sqrt{2} < x < 5\} \)
d) Reta indo para a esquerda até \( \frac{1}{2} \), com ponto fechado.
\( \{x \in \mathbb{R} \mid x \leq \frac{1}{2} \} \)
Resumo: A leitura correta de gráficos na reta real exige atenção ao tipo de ponto (aberto ou fechado) e à direção do traçado. A notação de conjuntos permite representar com precisão esses intervalos.
🧠 Mapas Mentais de Matemática