Lista de Exercícios com Solução Triângulos Isósceles

Triângulos Isósceles: O que é, exercícios e propriedades

Exercício 01 – Em cada caso abaixo, o triângulo ABC é isósceles com AB ≡ AC. Calcule x e y

a)

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]

b)

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]

Exercício 02 – O triângulo ABC é isósceles de base AC. Sabendo que A mede x + 30° e C mede 2x – 20°, determine x.

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]

Exercício 03 – O triângulo ABC é isósceles de base BC. Determine, em cada caso, o valor de x.

a)

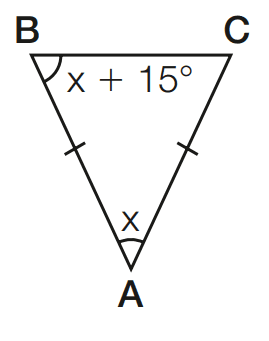
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

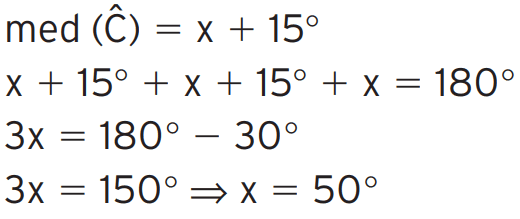
[/toggle]

b)

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]

c)

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

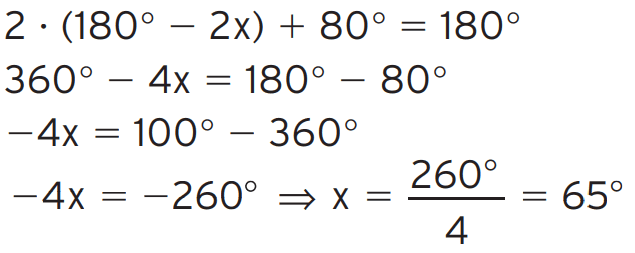
[/toggle]

Exercício 04 – Em um triângulo isósceles, um ângulo externo adjacente à base mede 130°. Determine os ângulos do triângulo.

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

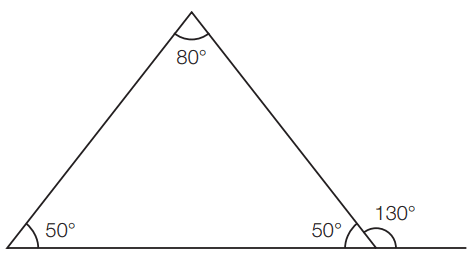
Resposta: 50°, 50°, 80°

[/toggle]

Exercício 05 – O triângulo PQR é isósceles de base QR. Observe a figura e determine x e y.

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

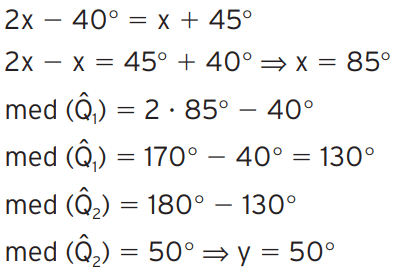
[/toggle]

Exercício 06 – Considerando que segmentos com marcas iguais são congruentes, determine x em cada figura.

a)

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

O triângulo ABC é isósceles retângulo. Então: med (A) = med (C) = 45°
Em C, temos ângulos opostos pelo vértice.
Então, no triângulo CDE, med (C) 5= 45° e med(D) = 75°. Portanto, med (E) = 60°.
Em E, os ângulos são suplementares.
Portanto, x = 120°.

[/toggle]

b)

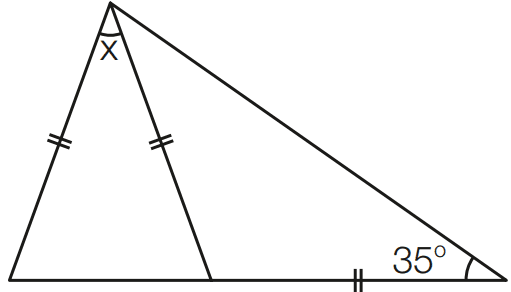
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

O triângulo ACD é isósceles.
Então: med (CAD) = 35° e med (ACD) = 110°.
Em C, os ângulos são suplementares.

No triângulo ABC, med (BCA) = 70°.
Como o triângulo ABC é isósceles,
med (B) = med (BCA) = 70°
Então: x + 70° + 70° = 180° ⇒ x = 40°.

[/toggle]

Exercício 07 – Em um triângulo isósceles de base DE, CS é bissetriz. Sabendo que DS mede 5 cm, determine ES = x e a medida de CSD.

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

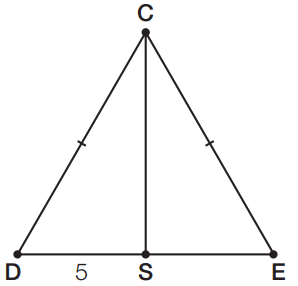
Se DS mede 5 cm, então SE = x = 5 cm e med (CSD) = 90°.

[/toggle]

Exercício 08 – Num triângulo isósceles ABC, com AB ≡ AC, AM é mediana. Se B mede 40°, determine a medida de MAC, x, e a de AMB, y.

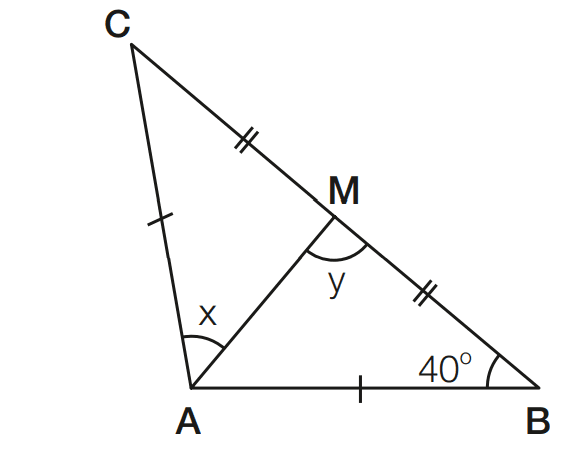
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]

Exercício 09 – A figura mostra um triângulo isósceles de base BC, em que  mede 80°. Sendo BD e CD bissetrizes dos ângulos ABC e A ˆ CB, res­pectivamente, calcule o valor de x.

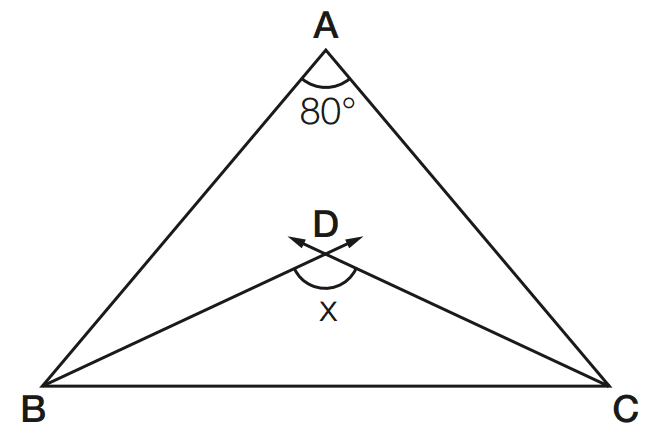
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]

A geometria é uma área fundamental da matemática, dedicada ao estudo das formas, tamanhos e propriedades de figuras no plano e no espaço.