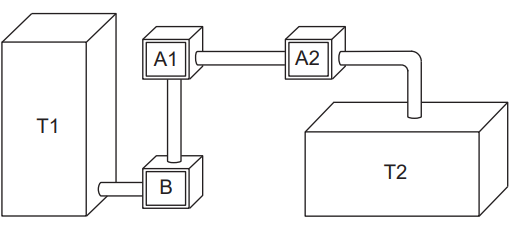
Um processo de aeração, que consiste na introdução de ar num líquido, acontece do seguinte modo: uma bomba B retira o líquido de um tanque T1 e o faz passar pelo aerador A1, que aumenta o volume do líquido em 15%, e em seguida pelo aerador A2, ganhando novo aumento de volume de 10%. Ao final, ele fica armazenado num tanque T2, de acordo com a figura.
Os tanques T1 e T2 são prismas retos de bases retangulares, sendo que a base de T1 tem comprimento \(c\) e largura \(L\), e a base de T2 tem comprimento \(\tfrac{c}{2}\) e largura \(2L\).
Para finalizar o processo de aeração sem derramamento do líquido em T2, o responsável deve saber a relação entre a altura da coluna de líquido que já saiu de T1, denotada por \(x\), e a altura da coluna de líquido que chegou a T2, denotada por \(y\).
A equação que relaciona as medidas das alturas \(y\) e \(x\) é dada por
- A) \(y = 1{,}265\,x\)
- B) \(y = 1{,}250\,x\)
- C) \(y = 1{,}150\,x\)
- D) \(y = 1{,}125\,x\)
- E) \(y = x\)
Mostrar / esconder solução passo a passo
T2 tem base \(A_{2}=\dfrac{c}{2}\cdot 2L=cL\) (mesma área!).
A2 aumenta \(10\%\): \(V_{2}=1{,}10\cdot V’ = 1{,}10\cdot1{,}15\,V_{1}= \mathbf{1{,}265}\,V_{1}\).






























