Questão 43
Uma caneca com água fervendo é retirada de um forno de micro-ondas. A temperatura \( T \), em grau Celsius, da caneca, em função do tempo \( t \), em minuto, pode ser modelada pela função \( T(t) = a + 80 \cdot b^t \), representada no gráfico a seguir.
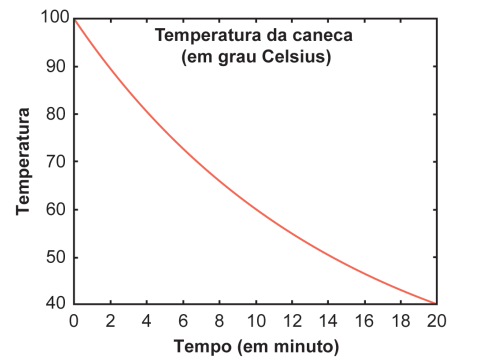
Os valores das constantes a e b são
- A) \( a = 20; \ b = \log(0{,}5) \)
- B) \( a = 100; \ b = 0{,}5 \)
- C) \( a = 20; \ b = (0{,}5)^{\frac{1}{10}} \)
- D) \( a = 20; \ b = \left(\frac{40}{80}\right)^{\frac{1}{10}} \)
- E) \( a = 20; \ b = 40 \)
1. Identificando o valor de a:
\[ T(0) = a + 80 \cdot b^0 = a + 80 = 100 \Rightarrow a = 20 \]
2. Usando outro ponto do gráfico (por exemplo, \( T(10) = 60 \)):
\[ T(10) = 20 + 80 \cdot b^{10} = 60 \Rightarrow 80 \cdot b^{10} = 40 \Rightarrow b^{10} = 0{,}5 \Rightarrow b = (0{,}5)^{1/10} \]
Resposta correta: alternativa C
[/toggle]












