Matriz: Diagonal Principal
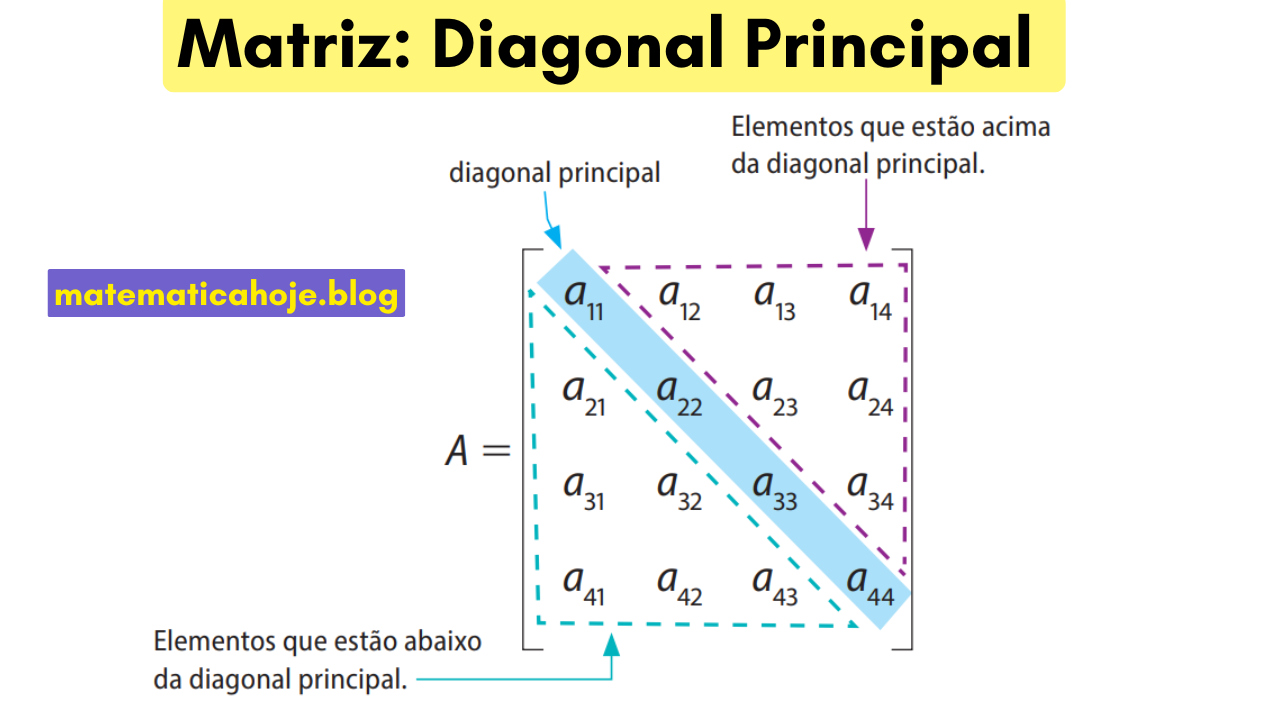
A diagonal principal de uma matriz quadrada é formada pelos elementos que possuem a mesma linha e coluna, ou seja, todos os elementos do tipo \(a_{ii}\). Ela é fundamental para o estudo de diversas propriedades das matrizes, como traço, determinantes e identificação de matrizes diagonais.
Definição
Seja a matriz quadrada \(A\) de ordem \(n\):
\[ A=\begin{bmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \dots & a_{nn} \end{bmatrix} \]
A sua diagonal principal é formada pelos elementos \(a_{11}, a_{22}, a_{33}, \dots, a_{nn}\).
Propriedades Importantes
- Traço da matriz: é a soma dos elementos da diagonal principal: \(tr(A) = a_{11}+a_{22}+…+a_{nn}\).
- Matriz diagonal: quando todos os elementos fora da diagonal principal são iguais a zero.
- Determinantes: no cálculo, os elementos da diagonal principal têm papel central nas regras de expansão.
Exemplo Resolvido
Exemplo: Considere a matriz \(M=\begin{bmatrix}2 & 1 & 3 \\ 0 & 5 & -1 \\ 4 & 2 & 7\end{bmatrix}\). Identifique a diagonal principal e calcule o traço.
Solução:
A diagonal principal é composta pelos elementos \(2,5,7\).
O traço é \(2+5+7=14\).
Lista de Exercícios
1) Identifique a diagonal principal da matriz \(A=\begin{bmatrix}1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9\end{bmatrix}\).
Ver solução
A diagonal principal é formada por \(1, 5, 9\).
2) Calcule o traço da matriz \(B=\begin{bmatrix}3 & 0 & -1 \\ 2 & 4 & 5 \\ 1 & 6 & 2\end{bmatrix}\).
Ver solução
\(tr(B)=3+4+2=9\).
3) Verifique se a matriz \(C=\begin{bmatrix}7 & 0 & 0 \\ 0 & 5 & 0 \\ 0 & 0 & 3\end{bmatrix}\) é diagonal.
Ver solução
Sim, pois todos os elementos fora da diagonal principal são iguais a zero.






















