Matriz Identidade
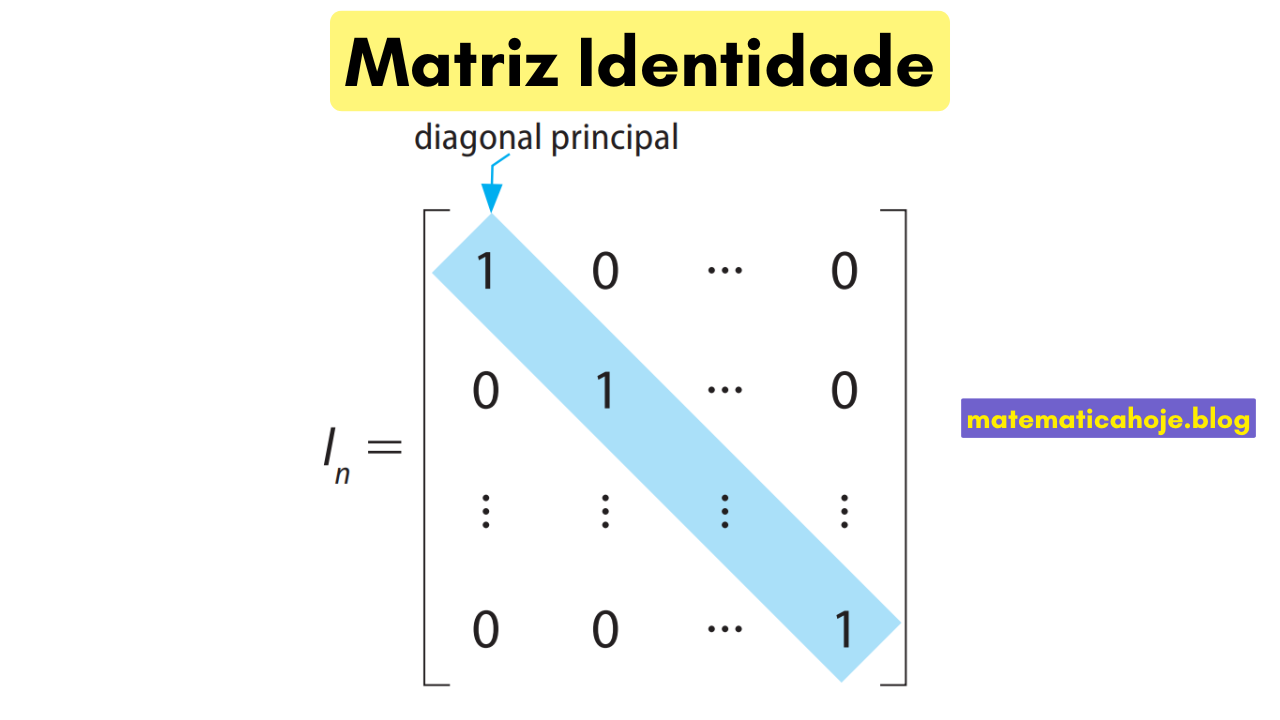
A matriz identidade é uma matriz quadrada em que todos os elementos da diagonal principal são iguais a 1 e todos os outros elementos são iguais a 0. Ela é representada por \(I_n\), onde \(n\) indica a ordem da matriz.
Definição
A matriz identidade de ordem \(n\) é dada por:
\[ I_n = \begin{bmatrix} 1 & 0 & 0 & \dots & 0 \\ 0 & 1 & 0 & \dots & 0 \\ 0 & 0 & 1 & \dots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \dots & 1 \end{bmatrix} \]
Propriedades da Matriz Identidade
- \(I_n\) é matriz quadrada de ordem \(n\).
- \(I_n \cdot A = A \cdot I_n = A\), para qualquer matriz quadrada \(A\) de ordem \(n\).
- É análoga ao número 1 na multiplicação de números reais.
- Seu determinante é sempre 1.
Exemplo Resolvido
Exemplo: Calcule \(I_3 \cdot A\), onde:
\[ I_3 = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}, \quad A = \begin{bmatrix} 2 & 3 & 4 \\ 1 & 0 & -1 \\ 5 & 2 & 6 \end{bmatrix} \]
Solução:
\(I_3 \cdot A = A\), logo o resultado é a própria matriz \(A\).
Exercícios de Fixação
1) Qual é a matriz identidade de ordem 2?
Ver solução
\(I_2 = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\)
2) Verifique se \(I_4 \cdot I_4 = I_4\).
Ver solução
Sim, a multiplicação de duas matrizes identidade resulta na própria matriz identidade.
3) Se \(B=\begin{bmatrix}4 & 5 \\ 7 & 8\end{bmatrix}\), calcule \(B \cdot I_2\).
Ver solução
O resultado é a própria matriz \(B\), ou seja, \(\begin{bmatrix}4 & 5 \\ 7 & 8\end{bmatrix}\).













