Matriz Linha

O que é uma Matriz Linha?

Chamamos de matriz linha toda matriz com apenas uma linha e \(n\) colunas. Seu formato é \(1 \times n\). Exemplos:

A = [ -3  2  7  0  5 ]  →  1 × 5
B = [ 4  0  -1 ]        →  1 × 3

Propriedades e observações

• Uma matriz linha pode ser vista como um vetor linha.
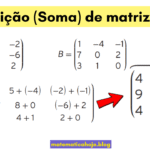
• A soma de duas matrizes linha \(1\times n\) é uma matriz linha \(1\times n\).
• A multiplicação por escalar mantém o formato (continua \(1\times n\)).
• O produto \(L\cdot C^\top\) com uma matriz coluna \(C\) \(n\times 1\) resulta em um escalar (produto escalar).
• O produto \(L\cdot M\) é definido apenas quando o número de colunas de \(L\) coincide com o número de linhas de \(M\).

Exemplos rápidos

1) Soma: \(L_1=[2\ -1\ 4]\) e \(L_2=[5\ 3\ 0]\). Então \(L_1+L_2=[7\ 2\ 4]\).

2) Produto por escalar: \(3\cdot[-2\ 1\ 5]=[-6\ 3\ 15]\).

3) Produto com coluna: \(L=[1\ 2\ 3]\), \(C=\begin{bmatrix}4\\0\\-1\end{bmatrix}\). Logo \(LC=1\cdot4+2\cdot0+3\cdot(-1)=1\).

Exercícios (múltipla escolha)

1) Qual é a ordem de \(L=[-3\ 2\ 7\ 0\ 5]\)?

1. \(5\times 1\)
2. \(1\times 5\)
3. \(5\times 5\)
4. \(1\times 3\)

2) Se \(L_1=[4\ 0\ -1]\) e \(L_2=[-2\ 3\ 5]\), então \(L_1+L_2\) é:

1. \([2\ 3\ 4]\)
2. \([6\ 3\ 4]\)
3. \([2\ 3\ -6]\)
4. \([2\ -3\ 6]\)

3) Seja \(L=[1\ -2\ 4\ 3]\). O produto por \(-2\) é:

1. \([-2\ 4\ -8\ -6]\)
2. \([2\ -4\ 8\ 6]\)
3. \([-2\ -4\ 8\ 6]\)
4. \([-2\ 4\ 8\ -6]\)

4) Dadas \(L=[2\ 1\ 0]\) e \(C=\begin{bmatrix}3\\-1\\5\end{bmatrix}\), calcule \(LC\).

1. \(1\)
2. \(6\)
3. \(-1\)
4. \(3\)

5) Para existir o produto \(L\cdot M\), com \(L\) matriz linha \(1\times n\), qual deve ser a ordem de \(M\)?

1. \(n\times 1\)
2. \(1\times n\)
3. \(n\times m\)
4. \(m\times n\)

6) Assinale a alternativa verdadeira:

1. Toda matriz linha é diagonal
2. O produto de uma matriz linha \(1\times n\) por uma coluna \(n\times 1\) é uma matriz \(1\times 1\)
3. Somar duas matrizes linha gera uma matriz coluna
4. Uma matriz linha não pode ser multiplicada por escalar

Para continuar estudando

Materiais úteis do blog: