Matriz Oposta
A matriz oposta é um conceito fundamental no estudo de álgebra matricial. Essa operação é cobrada no ENEM e em diversos concursos e serve de base para outras propriedades.
O que é a matriz oposta?
Dada uma matriz \(A=(a_{ij})\), chamamos de matriz oposta a matriz \(B=(b_{ij})\) tal que
Exemplo prático
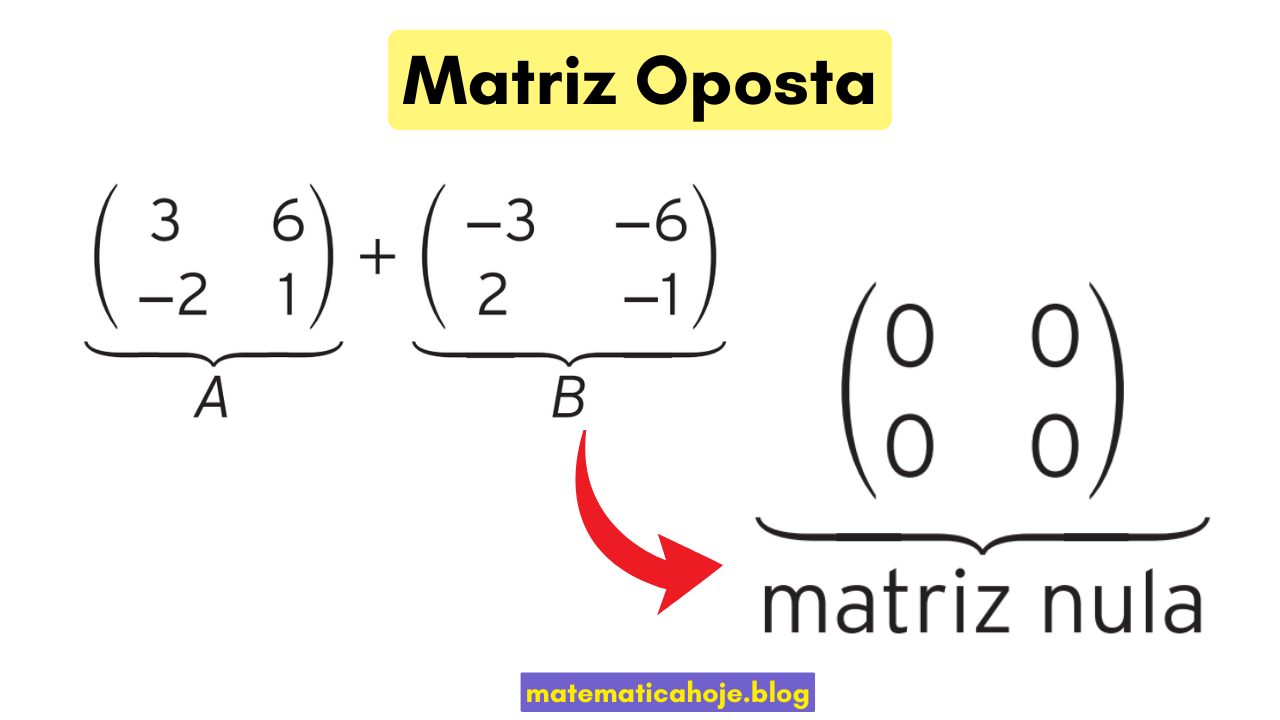
Considere a matriz:
\( A=\begin{bmatrix} 3 & 6\\[-2pt] -2 & 1 \end{bmatrix} \)
A matriz oposta de \(A\) é:
\( B=\begin{bmatrix} -3 & -6\\[-2pt] 2 & -1 \end{bmatrix} \)
Ao somarmos \(A+B\), obtemos a matriz nula:
\( A+B=\begin{bmatrix} 0 & 0\\[-2pt] 0 & 0 \end{bmatrix} \)
Baixe o eBook Fórmulas Matemática e tenha um guia completo de estudos.
Exercícios Resolvidos
Exercício 1: Determine a matriz oposta de \( M=\begin{bmatrix} 5 & -4\\ 2 & 7 \end{bmatrix} \).
Mostrar solução
Basta trocar o sinal de cada elemento:
\( M_{\text{op}}=\begin{bmatrix} -5 & 4\\ -2 & -7 \end{bmatrix} \).
Exercício 2: Verifique se \(B\) é a oposta de \(A\):
\( A=\begin{bmatrix} -1 & 3\\ 4 & -2 \end{bmatrix}, \quad
B=\begin{bmatrix} 1 & -3\\ -4 & 2 \end{bmatrix}. \)
Mostrar solução
Cada entrada de \(B\) é o oposto da correspondente em \(A\). Logo, \(B=-A\) e \(A+B=\mathbf{0}\).
Conclusão
A matriz oposta é simples e essencial para dominar listas de exercícios e operações matriciais. Explore também a adição de matrizes para consolidar o conteúdo.
Continue seus estudos com nossos materiais:






















