Matrizes
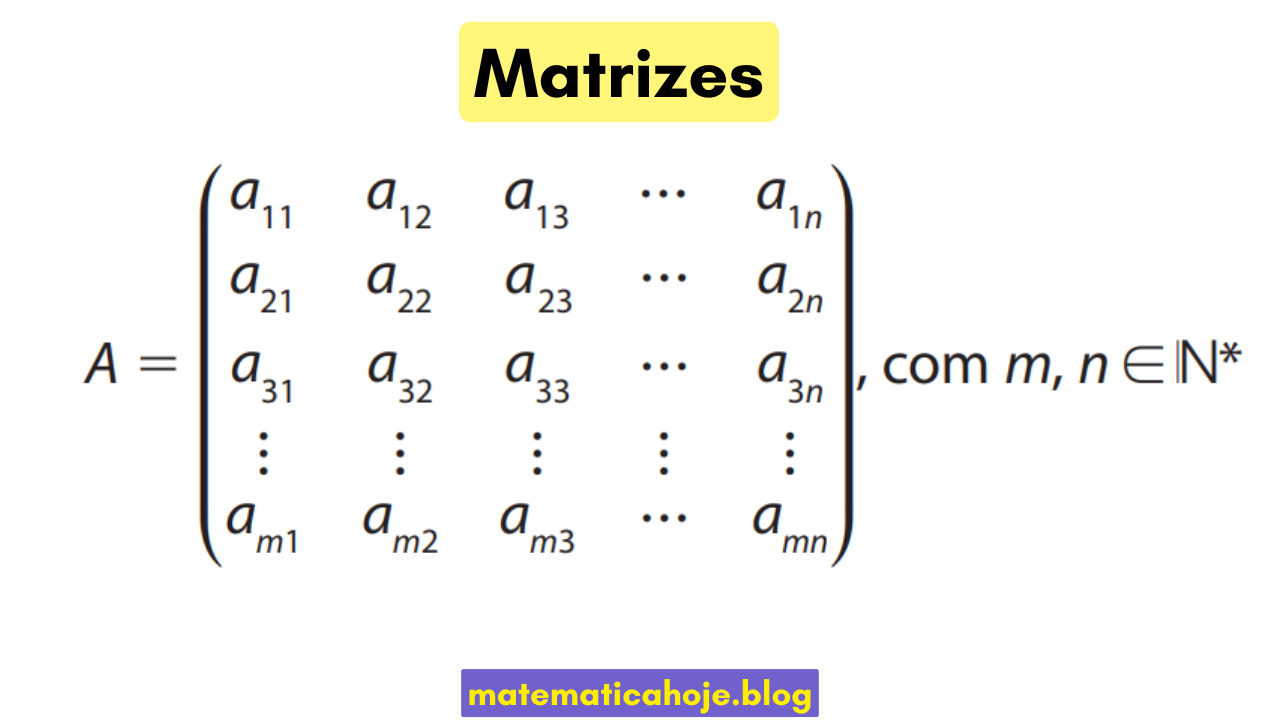
As matrizes são tabelas formadas por números, símbolos ou expressões, organizadas em linhas e colunas. Cada posição da matriz é chamada de elemento e é identificada por dois índices: a linha e a coluna.
Definição: Uma matriz \(A\) de ordem \(m \times n\) é representada por:
\[ A = \begin{bmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \dots & a_{mn} \end{bmatrix} \]
com \(m, n \in \mathbb{N}^*\).
Elementos Principais
- Ordem: número de linhas (m) e colunas (n).
- Elemento: indicado por \(a_{ij}\), sendo \(i\) a linha e \(j\) a coluna.
- Matriz quadrada: quando \(m=n\).
Tipos de Matrizes
- Matriz linha: possui apenas uma linha.
- Matriz coluna: possui apenas uma coluna.
- Matriz quadrada: número de linhas = número de colunas.
- Matriz diagonal: matriz quadrada com elementos diferentes de zero apenas na diagonal principal.
- Matriz identidade: matriz quadrada com 1 na diagonal principal e 0 nos demais elementos.
- Matriz nula: todos os elementos são iguais a 0.
Operações com Matrizes
Adição
Somamos elementos correspondentes de duas matrizes de mesma ordem.
Multiplicação por escalar
Multiplica-se cada elemento da matriz pelo número real dado.
Multiplicação de Matrizes
Se \(A\) é \(m \times n\) e \(B\) é \(n \times p\), então \(AB\) será \(m \times p\). Cada elemento é obtido pelo produto escalar da linha de \(A\) com a coluna de \(B\).
Matriz transposta
Trocam-se as linhas pelas colunas.
Exemplo Resolvido
Exemplo: Seja \(A=\begin{bmatrix}1 & 2 \\ 3 & 4\end{bmatrix}\) e \(B=\begin{bmatrix}0 & 1 \\ 5 & -2\end{bmatrix}\). Calcule \(A+B\).
Solução:
\[ A+B=\begin{bmatrix}1+0 & 2+1 \\ 3+5 & 4+(-2)\end{bmatrix}= \begin{bmatrix}1 & 3 \\ 8 & 2\end{bmatrix} \]
Lista de Exercícios
1) Dada a matriz \(M=\begin{bmatrix}2 & 4 \\ -1 & 3\end{bmatrix}\), determine sua transposta.
Ver solução
\[ M^T=\begin{bmatrix}2 & -1 \\ 4 & 3\end{bmatrix} \]
2) Seja \(A=\begin{bmatrix}1 & 2 \\ 0 & 1\end{bmatrix}\). Calcule \(2A\).
Ver solução
\[ 2A=\begin{bmatrix}2 & 4 \\ 0 & 2\end{bmatrix} \]
3) Multiplique \(A=\begin{bmatrix}1 & 0 \\ 2 & 1\end{bmatrix}\) por \(B=\begin{bmatrix}3 & 1 \\ 0 & 2\end{bmatrix}\).
Ver solução
\[ AB=\begin{bmatrix}1\cdot 3 + 0\cdot 0 & 1\cdot 1 + 0\cdot 2 \\ 2\cdot 3 + 1\cdot 0 & 2\cdot 1 + 1\cdot 2\end{bmatrix} =\begin{bmatrix}3 & 1 \\ 6 & 4\end{bmatrix} \]






















