Estudar múltiplos e divisores é fundamental para desenvolver uma compreensão sólida dos números e suas propriedades, além de facilitar a resolução de problemas em diversas áreas da matemática. Neste material, apresentamos uma lista de exercícios com soluções detalhadas, abordando conceitos essenciais como divisibilidade, números primos, fatoração, múltiplos e o mínimo múltiplo comum (MMC), divisores e o máximo divisor comum (MDC). A proposta é fortalecer o entendimento e a aplicação prática de cada tópico, fornecendo explicações passo a passo para facilitar o aprendizado.
Esses exercícios são organizados de forma progressiva para ajudar tanto na identificação de múltiplos e divisores, quanto na resolução de problemas que envolvem cálculos com MMC e MDC. Então, prepare-se para colocar em prática os conceitos e ganhar confiança para enfrentar desafios mais complexos!
01 – (Saresp) O teatro Martins Pena tem 243 poltronas. O número de poltronas do teatro
equivale a
a) 34
b) 35
c) 36
d) 37
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
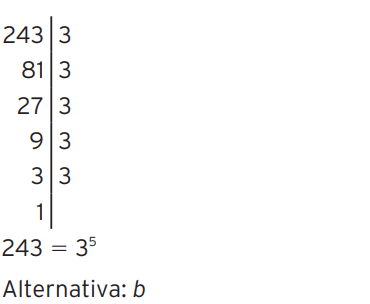
[/toggle]
02 – (UFRN) Duas escolas, X e Y, decidiram organizar uma gincana estudantil na qual os alunos devem formar todas as equipes com o mesmo número de componentes. Foram selecionados 49 alunos da escola X e 63 alunos da escola Y. Cada aluno deve participar de apenas uma equipe. Assim, o número de equipes participantes das escolas X e Y será, respectivamente:
a) 7 e 9
b) 6 e 9
c) 8 e 9
d) 7 e 8
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
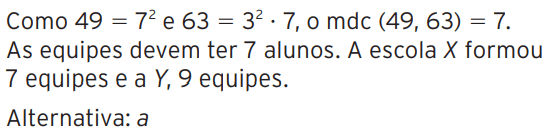
[/toggle]
03 – (Saresp) Paulão trabalha na seção de embalagens de bolinhas de gude. Ele só usa embalagens de dois tipos: caixa azul, para 6 bolinhas, ou caixa verde, para 8 bolinhas. Paulão calculou que, com a quantidade de bolinhas produzida sexta-feira passada, ele poderia ter usado apenas caixas azuis, sem que sobrasse nenhuma bolinha. Pensando mais um pouco, ele observou que, se usasse apenas as caixas verdes, teria acontecido o mesmo!
Assinale a alternativa que mostra o número de bolinhas que Paulão embalou nessa sexta-feira.
a) 102.
b) 120.
c) 126.
d) 184
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
04 – (UEL-PR) Considere dois rolos de barbante, um com 96 m e outro com 150 m de comprimento. Pretende-se cortar todo o barbante dos dois rolos em pedaços de mesmo comprimento. O menor número de pedaços que poderá ser obtido é:
a) 38
b) 41
c) 43
d) 52
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
05 – (Obmep) Mônica e seu namorado foram assistir a uma peça de teatro. O auditório era organizado em fileiras paralelas ao palco, todas com o mesmo número de cadeiras dispostas lado a lado. Eles se sentaram um ao lado do outro nos dois últimos lugares vagos. Mônica percebeu que havia, no total, 14 pessoas nas fileiras à sua frente e 21 pessoas nas fileiras atrás da sua. Quantas cadeiras havia no auditório?
a) 37
b) 38
c) 40
d) 42
e) 49
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
06 – (UFRN) Para os festejos natalinos, uma fábrica de doces lançará uma caixa de chocolates. O número de chocolates poderá ser dividido igualmente (sem fracioná-los) entre 2, 3, 4, 5 e 6 pessoas, não havendo sobra. O menor número de chocolates que essa caixa deverá conter será:
a) 180
b) 120
c) 60
d) 30
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
07 – (Fatec-SP) Um certo planeta possui dois satélites naturais (Lua A e Lua B); o planeta gira em torno do Sol e os satélites, em torno do planeta, de forma que os alinhamentos são
os seguintes:
- Sol-planeta-Lua A: ocorre a cada 18 anos;
- Sol-planeta-Lua B: ocorre a cada 48 anos.
Se hoje ocorrer o alinhamento Sol-planeta-Lua A-Lua B, então o fenômeno se repetirá daqui a:
a) 48 anos.
b) 66 anos.
c) 96 anos.
d) 144 anos.
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
08 – (UFSE) Três ônibus A, B e C partem simultaneamente do Terminal Rodoviário de Aracaju para três cidades distintas da região metropolitana. Sabe-se que A torna a partir do terminal a cada 40 minutos; B, a cada 60 minutos; e C, a cada 90 minutos.
Nessas condições, quanto tempo, em horas, terá decorrido até que os três ônibus partam novamente juntos desse terminal?
a) 2
b) 4
c) 6
d) 8
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
09 – (UEL-PR) Em 1982 ocorreu uma conjunção entre os planetas Júpiter e Saturno, o que
significa que podiam ser vistos bem próximos um do outro quando avistados da Terra. Se Júpiter e Saturno dão uma volta completa ao redor do Sol aproximadamente a cada 12 e 30 anos, respectivamente, em qual dos anos seguintes ambos estiveram em conjunção no céu da Terra?
a) 1840
b) 1852
c) 1864
d) 1922
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
10 – (UFMG) Calculando o máximo divisor comum dos números 756 e 2 205, a soma dos algarismos dele é igual a:
a) 3
b) 8
c) 9
d) 13
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
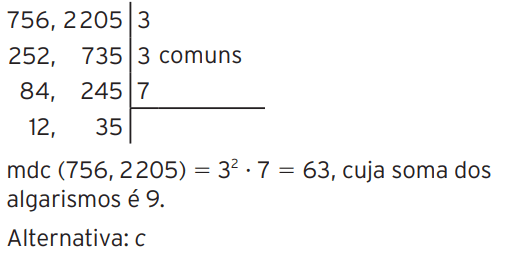
[/toggle]
11 – Pense e responda:
a) Se um número é múltiplo de 4 e de 6, então ele é múltiplo de 24?
b) Que números de dois algarismos são divisíveis por 4 e por 6?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]

























