Números Complexos — Definição, Operações, Forma Polar e Exercícios

Atualizado em 23 de agosto de 2025 • Leitura: ~16 min • Conteúdo com teoria, exemplos e exercícios

📌 Mapas Mentais 📘 10 eBooks 🧮 Banco de Questões 🎯 ENEM Matemática 📣 Canais Oficiais

O que são números complexos?

Um número complexo é escrito como \(z=a+bi\), com \(a,b\in\mathbb{R}\) e \(i\) tal que \(i^2=-1\). A parte \(a\) é a parte real \(\Re(z)\) e \(b\) a parte imaginária \(\Im(z)\).

\[ \mathbb{C}=\{a+bi\mid a,b\in\mathbb{R}\},\quad i^2=-1. \]

Os números reais surgem quando \(b=0\). Já os puramente imaginários têm \(a=0\).

Conexões: revise os reais, racionais e irracionais para a base conceitual.

Operações na forma algébrica

Soma/Subtração

\((a+bi)\pm(c+di)=(a\pm c)+(b\pm d)i\).

Produto

\[ (a+bi)(c+di)=(ac-bd)+(ad+bc)i. \]

Conjugado e divisão

O conjugado de \(z=a+bi\) é \(\overline{z}=a-bi\). Para dividir, multiplique numerador e denominador pelo conjugado do denominador:

\[ \frac{a+bi}{c+di}=\frac{(a+bi)(c-di)}{c^2+d^2} =\frac{ac+bd}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}i. \]

Plano complexo (Argand–Gauss)

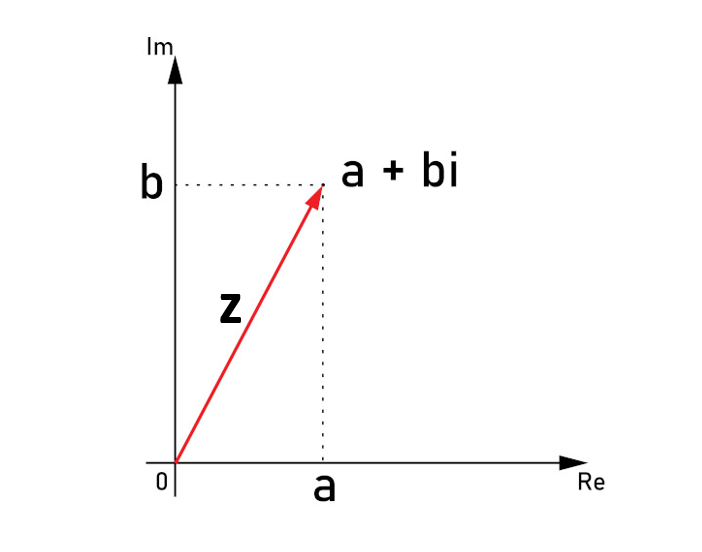
Representamos \(z=a+bi\) como o ponto \((a,b)\) em um plano cartesiano: eixo horizontal = parte real; eixo vertical = parte imaginária.

Distância à origem = módulo: \( |z|=\sqrt{a^2+b^2} \).

Módulo, argumento e conjugado

Módulo: \( |z|=\sqrt{a^2+b^2} \).

Argumento (ângulo): \( \arg(z)=\theta=\operatorname{atan2}(b,a) \) (em radianos).

Conjugado: \( \overline{z}=a-bi \) e \(z\,\overline{z}=|z|^2\).

Em geral, \( \cos\theta=\dfrac{a}{|z|} \) e \( \sin\theta=\dfrac{b}{|z|} \) (com \(z\neq 0\)).

Forma trigonométrica/polar

Qualquer \(z\neq 0\) pode ser escrito como

\[ z = |z|(\cos\theta + i\sin\theta)=r(\cos\theta+i\sin\theta), \]

em que \(r=|z|\) e \(\theta=\arg(z)\). Nessa forma, multiplicação e divisão ficam simples:

\[ r_1(\cos\alpha+i\sin\alpha)\cdot r_2(\cos\beta+i\sin\beta) = r_1r_2\big(\cos(\alpha+\beta)+i\sin(\alpha+\beta)\big). \]

Fórmula de Euler e De Moivre

A fórmula de Euler liga exponenciais e trigonometria:

\[ e^{i\theta}=\cos\theta+i\sin\theta. \]

O teorema de De Moivre fornece potências na forma polar:

\[ \big(\cos\theta+i\sin\theta\big)^n=\cos(n\theta)+i\sin(n\theta),\quad n\in\mathbb{Z}. \]

Raízes da unidade

As soluções de \(z^n=1\) são \(n\) pontos igualmente espaçados no círculo unitário:

\[ z_k=\cos\frac{2\pi k}{n}+i\sin\frac{2\pi k}{n}=e^{i\frac{2\pi k}{n}},\quad k=0,1,\dots,n-1. \]

Exemplos Resolvidos

Exemplo 1 — Produto e divisão

Enunciado: Calcule \((2+3i)(1-4i)\) e \(\dfrac{2+3i}{1-4i}\).

Solução

Produto: \((2+3i)(1-4i)=2-8i+3i-12i^2=2-5i+12=14-5i\).

Divisão: \(\dfrac{2+3i}{1-4i}=\dfrac{(2+3i)(1+4i)}{1+16}=\dfrac{2+8i+3i+12i^2}{17}=\dfrac{-10+11i}{17}=-\dfrac{10}{17}+\dfrac{11}{17}i\).

Exemplo 2 — Módulo e argumento

Enunciado: Para \(z=-1+\sqrt{3}\,i\), encontre \(|z|\) e \(\arg(z)\).

Solução

\(|z|=\sqrt{(-1)^2+(\sqrt{3})^2}=\sqrt{1+3}=2\). Como \(a=-1<0\) e \(b=\sqrt{3}>0\), \(z\) está no 2º quadrante; \(\theta=2\pi/3\).

Exemplo 3 — Forma polar e potência

Enunciado: Escreva \(z=\sqrt{2}+i\sqrt{2}\) na forma polar e calcule \(z^3\).

Solução

\(|z|=\sqrt{2+2}=2\), \(\theta=\pi/4\). Logo \(z=2(\cos\frac{\pi}{4}+i\sin\frac{\pi}{4})\). Pela De Moivre, \(z^3=2^3\big(\cos\frac{3\pi}{4}+i\sin\frac{3\pi}{4}\big)=8\left(-\frac{\sqrt{2}}{2}+i\frac{\sqrt{2}}{2}\right)=-4\sqrt{2}+4\sqrt{2}\,i\).

Exercícios Propostos

Calcule \((3-2i)+(5+7i)\) e \((4+i)-(6-3i)\).

Determine \(|z|\), \(\arg(z)\) e \(\overline{z}\) para \(z=1- i\).

Escreva \(z=-\sqrt{3}+i\) na forma polar \(r(\cos\theta+i\sin\theta)\).

Use De Moivre para calcular \(\big(\cos\frac{\pi}{6}+i\sin\frac{\pi}{6}\big)^5\).

Encontre todas as soluções de \(z^4=1\).

Converta \(\dfrac{1+i}{1-i}\) para a forma \(a+bi\).

Resolva \(x^2+1=0\) em \(\mathbb{C}\).

Mostre que \(z\overline{z}=|z|^2\) para \(z=a+bi\).

Gabarito

1) \( (3-2i)+(5+7i)=8+5i\); \( (4+i)-(6-3i)=-2+4i\).

2) Para \(z=1-i\): \(|z|=\sqrt{2}\), \(\arg(z)=-\pi/4\) (ou \(7\pi/4\)), \(\overline{z}=1+i\).

3) \(r=\sqrt{(\sqrt{3})^2+1^2}=2\), \(\theta=5\pi/6\) ⇒ \(2(\cos\frac{5\pi}{6}+i\sin\frac{5\pi}{6})\).

4) \(\cos\frac{5\pi}{6}+i\sin\frac{5\pi}{6}\) elevado a 5 ⇒ \(\cos\frac{5\pi}{6}\cdot5 + i\sin\frac{5\pi}{6}\cdot5=\cos\frac{5\pi}{6}\)??? (usar De Moivre): \((\cos\theta+i\sin\theta)^n=\cos(n\theta)+i\sin(n\theta)\). Para \(\theta=\pi/6\) e \(n=5\) ⇒ \(\cos\frac{5\pi}{6}+i\sin\frac{5\pi}{6}= -\frac{\sqrt{3}}{2}+\frac{1}{2}i\).

5) \(z_k=e^{i\frac{2\pi k}{4}}=\{1,i,-1,-i\}\).

6) \(\dfrac{1+i}{1-i}=\dfrac{(1+i)^2}{1+1}=\dfrac{1+2i+i^2}{2}=\dfrac{2i}{2}=i\).

7) \(x=\pm i\).

8) \((a+bi)(a-bi)=a^2+b^2=|z|^2\).