Questão 14 – OBMEP 2024
Laura tem 6 cubos iguais, exceto pela cor, sendo 2 vermelhos, 2 amarelos e 2 verdes. Ela coloca esses 6 cubos uns sobre os outros formando uma pilha. Um exemplo de como ela pode fazer isso está mostrado na figura. Quantas pilhas diferentes Laura pode fazer de modo que os cubos vermelhos não ocupem a base, nem o topo da pilha?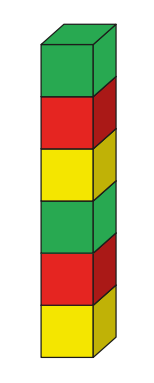
Alternativas:
- (A) 36
- (B) 6
- (C) 20
- (D) 120
- (E) 12
Ver Solução
Entendendo o enunciado:
Laura tem 6 cubos, sendo 2 de cada cor. Ela deseja empilhá-los de modo que os cubos vermelhos não estejam na base nem no topo da pilha.
Passo 1: Determinar as posições possíveis dos cubos vermelhos:
As posições da pilha vão de 1ª (base) até 6ª (topo). Como os cubos vermelhos não podem ocupar a 1ª nem a 6ª posição, temos as posições 2ª a 5ª disponíveis para eles.
Escolhendo 2 posições entre essas 4, temos:
\( \binom{4}{2} = 6 \) maneiras
Passo 2: Distribuir os outros 4 cubos (2 verdes e 2 amarelos) nas 4 posições restantes:
O número de anagramas com 2 verdes e 2 amarelos é:
\( \frac{4!}{2! \cdot 2!} = 6 \)
Conclusão:
Pelo Princípio Multiplicativo:
\(6 \text{ (posições para vermelhos)} \times 6 \text{ (formas de organizar verdes e amarelos)} = 36\)
Gabarito: Letra A
🧠 Mapas Mentais de Matemática





















