OBMEP 2024 – Nível 2 – Questão 13
Enunciado:
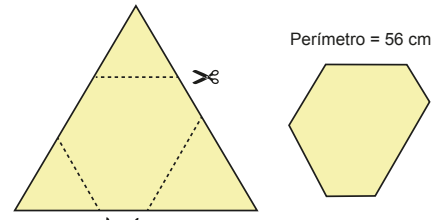
Pedro tem uma folha de papel com o formato de um triângulo equilátero de 28 cm de lado. Ele cortou três triângulos equiláteros dos cantos da sua folha, como na figura, e o hexágono resultante ficou com 56 cm de perímetro. Qual é a soma dos perímetros dos triângulos recortados?
Alternativas:
- (A) 93 cm
- (B) 111 cm
- (C) 120 cm
- (D) 84 cm
- (E) 102 cm
Ver Solução
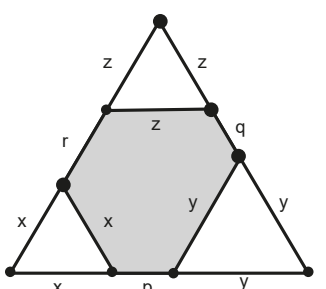
Entendendo o enunciado: Temos um triângulo equilátero de lado 28 cm, do qual foram recortados 3 triângulos menores, também equiláteros, um em cada canto. A figura resultante é um hexágono de perímetro 56 cm.
1. Perímetro do triângulo original:
Como cada lado tem 28 cm, o perímetro é:
\( 3 \times 28 = 84 \) cm
2. Perímetro do hexágono:
Foi informado que o hexágono formado após os recortes tem 56 cm de perímetro.
3. Diferença entre os perímetros:
O valor perdido do perímetro original, ou seja, a soma dos lados que foram substituídos pelos recortes, é:
\( 84 – 56 = 28 \) cm
4. Perímetro dos triângulos recortados:
Cada triângulo recortado teve três lados, dos quais apenas um ficou no hexágono (um lado interno), e os outros dois são somados ao perímetro dos recortes. Assim, a soma total dos perímetros dos 3 triângulos é:
\( 3 \times 28 = 84 \) cm
Alternativa correta: (D) 84 cm
🧠 Mapas Mentais de Matemática





















