Paralelepípedo retângulo — Volume, Áreas e Diagonal Espacial
Resumo direto com fórmulas, exemplos passo a passo e exercícios. As contas aparecem em linhas separadas após a igualdade para leitura rápida.
Conceitos rápidos
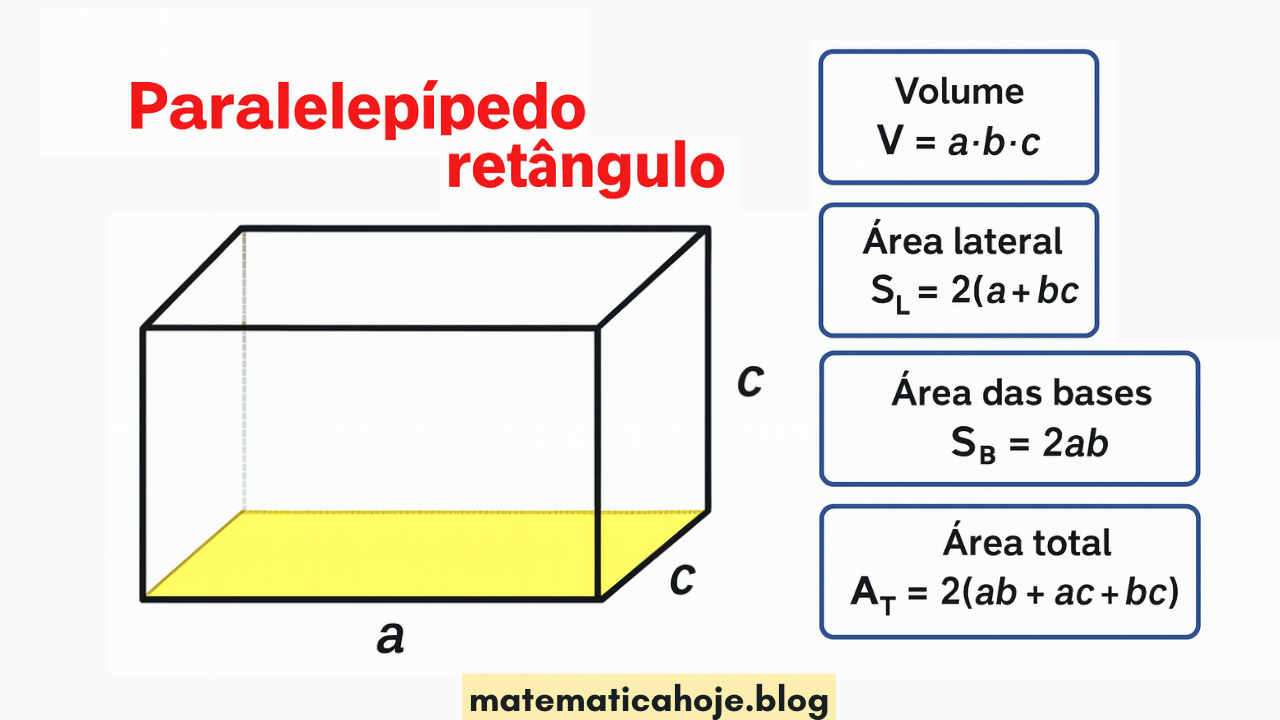
O paralelepípedo retângulo (ou prisma retangular) possui arestas perpendiculares de comprimentos a, b e c. Suas faces são retângulos em pares congruentes. Tema frequente no ENEM Matemática. Para revisão visual, veja os Mapas Mentais.
Fórmulas essenciais
Volume e Áreas
\( V = a\cdot b\cdot c \) | \( S_B = 2ab \) | \( S_L = 2(ac+bc) \) | \( A_T = 2(ab+ac+bc) \)
Diagonal espacial
\( d = \sqrt{a^2 + b^2 + c^2} \)
Depois pratique no Banco de Questões e confira a Coleção 10 eBooks.
Exemplos resolvidos (passo a passo)
Exemplo 1 — Volume
Enunciado. Para \( a=5\ \text{cm}\), \( b=3\ \text{cm}\), \( c=14\ \text{cm}\). Calcule o volume.
Ver solução
\( V = a\cdot b\cdot c \)
\( = 5\cdot 3\cdot 14 \)
\( = 15\cdot 14 \)
\( = 210\ \text{cm}^3 \)
Exemplo 2 — Área total
Enunciado. Um paralelepípedo tem \( a=4\ \text{cm}\), \( b=6\ \text{cm}\), \( c=10\ \text{cm}\). Determine \( A_T \).
Ver solução
\( A_T = 2(ab+ac+bc) \)
\( = 2(4\cdot 6 + 4\cdot 10 + 6\cdot 10) \)
\( = 2(24 + 40 + 60) \)
\( = 2\cdot 124 \)
\( = 248\ \text{cm}^2 \)
Exemplo 3 — Diagonal espacial
Enunciado. Calcule \( d \) para \( a=8\ \text{cm}\), \( b=6\ \text{cm}\), \( c=3\ \text{cm}\).
Ver solução
\( d = \sqrt{a^2 + b^2 + c^2} \)
\( = \sqrt{8^2 + 6^2 + 3^2} \)
\( = \sqrt{64 + 36 + 9} \)
\( = \sqrt{109} \)
\( \approx 10{,}44\ \text{cm} \)
📘 eBook Grátis — Fórmulas Matemática
Todas as fórmulas de Geometria Espacial, Planimetria e Álgebra — perfeito para revisão rápida.
➡️ Baixar AgoraExercícios — Paralelepípedo retângulo
Para treinar mais, acesse o Banco de Questões e a Coleção 10 eBooks.
1) Calcule \(V\) para \( a=7\ \text{cm}\), \( b=5\ \text{cm}\), \( c=3\ \text{cm}\).
Ver solução
\( = 7\cdot 5\cdot 3 \)
\( = 35\cdot 3 \)
\( = 105\ \text{cm}^3 \)
2) Encontre \(A_T\) para \( a=9\ \text{cm}\), \( b=4\ \text{cm}\), \( c=10\ \text{cm}\).
Ver solução
\( = 2(9\cdot 4 + 9\cdot 10 + 4\cdot 10) \)
\( = 2(36 + 90 + 40) \)
\( = 2\cdot 166 \)
\( = 332\ \text{cm}^2 \)
3) (Múltipla escolha) A diagonal espacial de \( a=6\), \( b=8\), \( c=24\) vale:
- 10 cm
- 26 cm
- \(2\sqrt{109}\) cm
- \(\sqrt{676}\) cm
Ver solução
\( = \sqrt{36+64+576} \)
\( = \sqrt{676} \)
\( = 26\ \text{cm} \) — alternativa D.
4) Determine \(S_L\) para \( a=12\ \text{cm}\), \( b=7\ \text{cm}\), \( c=5\ \text{cm}\).
Ver solução
\( = 2(12\cdot 5 + 7\cdot 5) \)
\( = 2(60 + 35) \)
\( = 2\cdot 95 \)
\( = 190\ \text{cm}^2 \)
5) (Múltipla escolha) Se apenas \( c \) é dobrado, o volume:
- permanece igual
- duplica
- quadruplica
- divide por 2
Ver solução
\( c \to 2c \Rightarrow V \to 2V \).
Alternativa B.













