Permutação Circular com Repetição: Entenda e Domine o Conceito

A permutação circular com repetição é um conceito avançado da análise combinatória, usado para calcular o número de formas distintas de organizar elementos repetidos em um formato circular. Esse tipo de permutação é essencial em situações onde as posições relativas entre os elementos importam, como em mesas redondas, colares ou coroas.

Neste artigo, você aprenderá o que é permutação circular com repetição, a fórmula utilizada, exemplos práticos e exercícios resolvidos. Vamos explorar esse tema de maneira simples e humanizada, trazendo o contexto da matemática para aplicações práticas do dia a dia.

Transforme seus estudos com o eBook Matemática Resumida: + de 90 Mapas Mentais de Matemática! Simplifique conceitos complexos, organize seus estudos e revise de forma prática e eficiente. Baixe agora e conquiste seus objetivos!

O Que é Permutação Circular com Repetição?

A permutação circular ocorre quando elementos são organizados em um círculo, e as posições dos elementos são consideradas relativas, ou seja, girar o círculo não cria uma nova permutação distinta. Quando há repetição de elementos no conjunto, o número de combinações únicas é ainda mais reduzido, pois reorganizar os itens idênticos não altera a disposição.

Fórmula da Permutação Circular com Repetição

A fórmula para calcular o número de permutações circulares com elementos repetidos é:

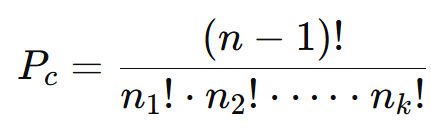
Onde:

• n: número total de elementos.
• n1, n2, …, nk: número de repetições de cada elemento.

📚 Quer aprofundar seus conhecimentos em Análise Combinatória e Probabilidade? Confira nossa recomendação dos melhores livros sobre o tema com exercícios resolvidos e dicas práticas. 👉Os melhores livros de Analise Combinatória e Probabilidade

Exemplo Prático 1: Organização de Bolas

Problema:

Temos 5 bolas, sendo 3 pretas (P) e 2 brancas (B). Quantas disposições distintas podemos criar ao organizá-las em um círculo?

Solução:

1. Identifique o total de elementos (n): 5.
2. Conte as repetições:
   • Bolas pretas (n₁): 3.
   • Bolas brancas (n₂): 2.
3. Substitua na fórmula:

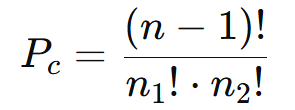
Substituindo os valores temos:

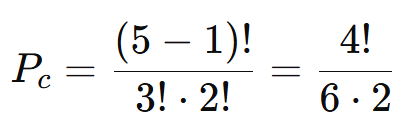
4. Calcule os fatoriais:
   • 4! = 4×3×2×1 = 24
   • 3! = 6.
   • 2! = 2.

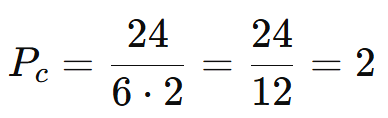
Resposta: Existem 2 arranjos distintos.

👉Entre no nosso canal do WhatsApp

📘 Todas as fórmulas de matemática em um só lugar! Baixe agora nosso eBook gratuito

Exemplo Prático 2: Formando um Colar

Problema:

Um colar é feito com 7 contas, sendo 4 vermelhas e 3 azuis. Quantas disposições únicas podem ser criadas?

Solução:

1. Total de contas (n): 7.
2. Repetições:
   • Contas vermelhas (n₁): 4.
   • Contas azuis (n₂): 3.
3. Aplique a fórmula:

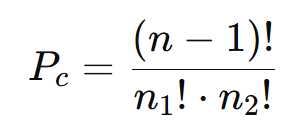
Substituindo os valores temos:

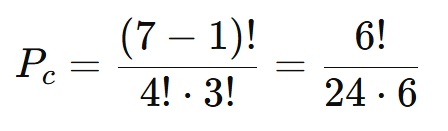
4. Calcule os fatoriais:
   • 6! = 720.
   • 4! = 24.
   • 3! = 6.

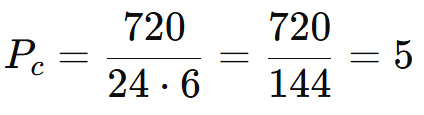
Resposta: Existem 5 disposições únicas para o colar.

Exemplo Prático 3: Formando um Colar

Quantas maneiras diferentes podemos organizar 7 flores em uma coroa circular, sendo 3 flores vermelhas e 3 flores brancas e uma rosa?

1 – Análise Combinatória – Permutação Circular com Repetição
Neste problema, estamos organizando 7 flores em uma coroa circular, sendo:

• 3 flores vermelhas,
• 3 flores brancas,
• 1 flor rosa.

Como a disposição é circular e há repetições, utilizamos a fórmula da Permutação Circular com Repetição:

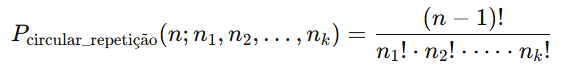
2 – Entendendo o Enunciado

1. Total de flores (n=7n = 7).
2. Repetições:
   • 3 flores vermelhas (n₁ = 3),
   • 3 flores brancas (n₂ = 3),
   • 1 flor rosa (n₃ = 1).

Aplicamos a fórmula considerando as repetições e a disposição circular.

3 – Cálculo

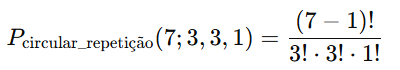
Calculamos os fatoriais:

(7−1)! = 6! = 720

3! = 6,

1! = 1.

Substituímos:

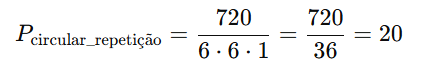
4 – Resposta
As 7 flores (3 vermelhas, 3 brancas e 1 rosa) podem ser organizadas em uma coroa circular de 20 maneiras diferentes.

Passo a Passo para Resolver Permutação Circular com Repetição

1. Determine o total de elementos (n) e as repetições:
   Conte todos os elementos do conjunto e identifique os que se repetem.
2. Subtraia 1 do total de elementos para considerar a forma circular:
   Isso elimina redundâncias causadas pela rotação do círculo.
3. Aplique a fórmula:
   Substitua os valores na fórmula da permutação circular com repetição.
4. Resolva os fatoriais:
   Faça os cálculos para encontrar o número final de disposições únicas.

Aplicações Práticas da Permutação Circular com Repetição

1. Design de Joias e Colares:
   Planejar padrões únicos para colares ou pulseiras circulares.
2. Eventos e Mesas Redondas:
   Organizar pessoas ou itens em mesas circulares.
3. Decoração e Arte:
   Criar padrões repetitivos em arranjos circulares.
4. Problemas de Lógica:
   Resolver quebra-cabeças envolvendo arranjos repetidos em círculos.

Resumo

A permutação circular com repetição é uma ferramenta essencial da permutação na da análise combinatória, permitindo calcular disposições únicas de elementos organizados em círculos, mesmo quando há repetições. Sua fórmula ajusta os cálculos para eliminar redundâncias causadas por rotações e repetições.

Com exemplos práticos e exercícios resolvidos, você agora tem as ferramentas necessárias para aplicar esse conceito em problemas de matemática e situações reais. Continue praticando e expandindo seu conhecimento!