Planificação do Cubo — redes, área e exercícios
Tudo sobre planificação do cubo: o que é, as 11 redes possíveis, como reconhecer se uma malha forma cubo, relação com área total do cubo, exemplos práticos e uma lista de exercícios (com gabarito).
1) O que é planificação do cubo?
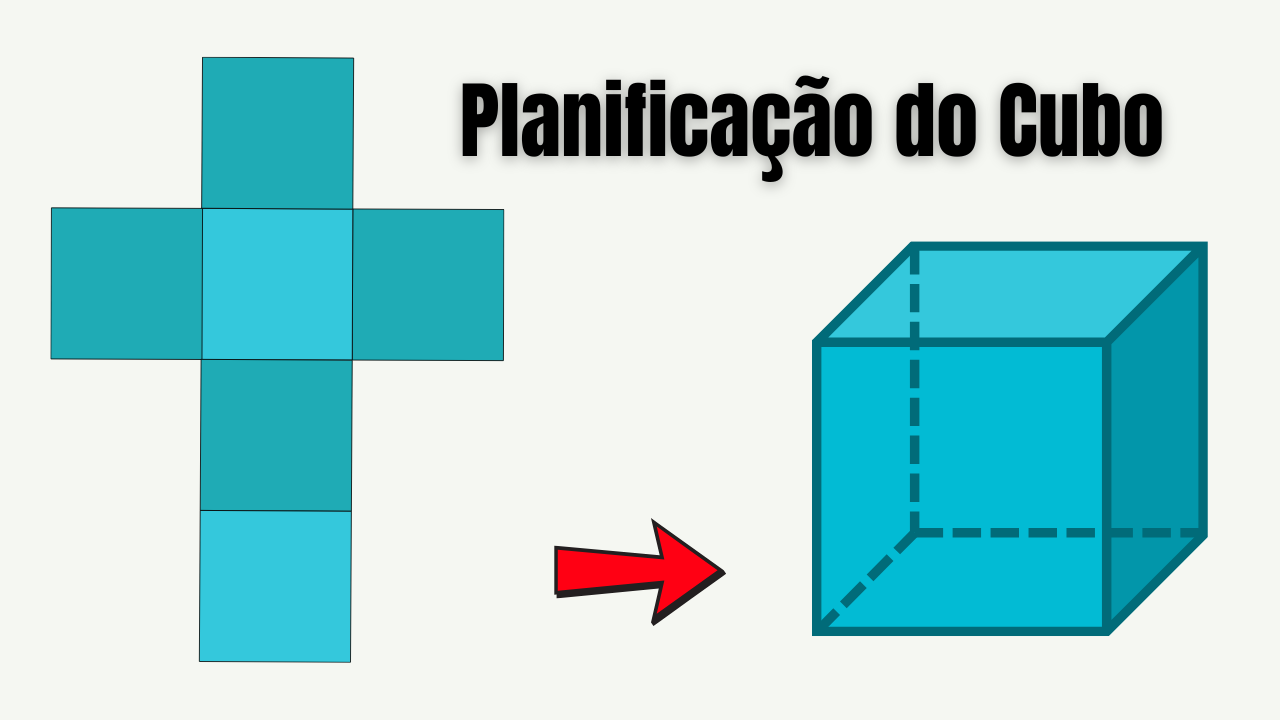
Planificação é a representação plana das faces do cubo (6 quadrados congruentes) posicionadas de forma que, ao dobrar nas arestas, formem o sólido. O cubo é um hexaedro regular (6 faces, 12 arestas, 8 vértices) e toda rede válida deve permitir que cada face toque exatamente quatro vizinhas ao ser montada.
Quantas planificações do cubo existem?
Existem 11 planificações distintas (não congruentes) para o cubo. Todas usam seis quadrados iguais. Muitas malhas parecidas não funcionam: ou criam sobreposição ao dobrar ou deixam lacunas.
2) Como reconhecer se a malha forma um cubo?
- Conectividade: os 6 quadrados precisam formar um único bloco (grafo conectado).
- Graus de adjacência: cada quadrado deve poder ter até 4 vizinhos na montagem; na malha plana, evite “cruzes” com braços longos que colidem ao dobrar.
- Teste mental de dobra: escolha um quadrado como base, dobre as faces adjacentes como paredes e verifique se sobra exatamente uma para virar “tampa”.
- Colisões: braços opostos muito longos podem se sobrepor no fechamento — nesses casos, a rede é inválida.
Relação direta com a área total do cubo
Qualquer planificação válida mostra, de uma vez, a área total do cubo: se a aresta tem comprimento \(a\), cada face tem área \(a^2\). Como são 6 faces, a área total é \(A_t=6a^2\). Se quiser apenas a área lateral (sem topo e base), conte 4 faces: \(A_l=4a^2\).
3) Passo a passo para montar um cubo a partir da planificação
- Escolha o quadrado central como “base”.
- Dobre as quatro faces adjacentes a 90° (viram paredes).
- Feche com a face restante (tampa). Se houver sobreposição ou falta de tampa, a planificação é inválida.
- Conferência: todas as arestas com mesmo comprimento e faces quadradas congruentes.
4) Exemplos práticos
Exemplo 1 — “cruz” clássica
Enunciado. A planificação em forma de cruz com uma fileira de 4 quadrados e dois anexos no 2º quadrado forma um cubo?
Ver solução
Exemplo 2 — braço duplo no mesmo lado
Enunciado. Uma fileira de 4 quadrados com dois quadrados anexos ao mesmo quadrado extremo funciona?
Ver solução
Exemplo 3 — calculando área pela planificação
Enunciado. A malha é válida e cada quadrado mede \(4\ \text{cm}\) de lado. Qual é a área total do cubo?
Ver solução
5) Erros comuns
- Contar 5 ou 7 quadrados — precisam ser 6 e congruentes.
- Ignorar sobreposição: braços que tentam fechar o mesmo lado do cubo.
- Confundir área lateral (4 faces) com área total (6 faces).
- Misturar medidas de arestas (cm, m) e áreas (cm², m²).
6) Exercícios sobre planificação do cubo
Enunciado. Uma planificação mostra 6 quadrados de lado \(a=3\ \text{cm}\). Calcule a área total do cubo.
Ver solução
\(A_t=6a^2=6\cdot9=\mathbf{54\ \text{cm}^2}\).Enunciado. Em uma rede válida, a área lateral do cubo deve corresponder a quantos quadrados?
Ver solução
A 4 quadrados (as “paredes”): \(\mathbf{A_l=4a^2}\).Enunciado. Uma malha apresenta 4 quadrados em linha e mais 2 quadrados anexos ao 2º da fileira (um acima e um abaixo). Ela forma um cubo?
Ver solução
Sim. É a “cruz clássica”: funciona e é uma das 11 redes.Enunciado. Cada quadrado da planificação tem área \(25\ \text{cm}^2\). Qual é o volume do cubo?
Ver solução
Lado \(a=\sqrt{25}=5\ \text{cm}\). Volume \(V=a^3=125\ \text{cm}^3\).Enunciado. Dê um critério simples para rejeitar rapidamente uma planificação.
Ver solução
Se houver dois quadrados “tampa” tentando fechar o mesmo lado (colisão ao dobrar) ou se a rede não for conectada, é inválida.
7) Questões de múltipla escolha (com gabarito em abre/fecha)
Uma planificação válida do cubo deve conter:
- A) 5 quadrados congruentes
- B) 6 quadrados não necessariamente iguais
- C) 6 quadrados congruentes
- D) 7 quadrados congruentes
Ver solução
Gabarito: C. O cubo tem 6 faces quadradas congruentes.Qual opção sempre indica rede inválida?
- A) Fileira de 4 quadrados com anexos opostos ao 2º quadrado
- B) Fileira de 4 quadrados com 2 anexos no mesmo extremo
- C) Cruz clássica
- D) Fileira de 3 quadrados com anexos nos três
Ver solução
Gabarito: B. Dois anexos no mesmo extremo tendem a colidir ao fechar o cubo.Se cada quadrado tem lado \(a\), então a área total lida na planificação é:
- A) \(4a^2\)
- B) \(5a^2\)
- C) \(6a^2\)
- D) \(a^3\)
Ver solução
Gabarito: C. Seis faces ⇒ \(6a^2\).Na planificação, a diagonal da face é \(d_f=a\sqrt{2}\). Se \(a=8\ \text{cm}\), então:
- A) \(d_f=8\ \text{cm}\)
- B) \(d_f=8\sqrt{2}\ \text{cm}\)
- C) \(d_f=16\ \text{cm}\)
- D) \(d_f=4\sqrt{2}\ \text{cm}\)
Ver solução
Gabarito: B. Diagonal do quadrado \(=a\sqrt{2}\).Uma planificação correta permite montar o cubo com:
- A) 3 faces opostas tocando-se
- B) Sobreposição de duas “tampas”
- C) Uma única “tampa” após erguer quatro paredes
- D) Duas partes desconectadas que se unem no final
Ver solução
Gabarito: C. A montagem correta ergue 4 paredes e fecha com 1 tampa.
8) Perguntas frequentes
| Quantas planificações do cubo existem? | São 11 redes diferentes (não congruentes), todas com 6 quadrados congruentes. |
|---|---|
| Como usar a planificação para calcular área? | Basta contar as faces: área de cada face \(=a^2\). Assim, \(A_t=6a^2\) e \(A_l=4a^2\). |
| Quais são os elementos do cubo? | 6 faces quadradas, 12 arestas, 8 vértices (hexaedro regular). |




























