Planificação do Prisma Triangular — guia completo
Entenda o que é a rede (net) do prisma triangular, como construir, quais são as medidas de cada parte e como usar a planificação para calcular área lateral, área total e volume.
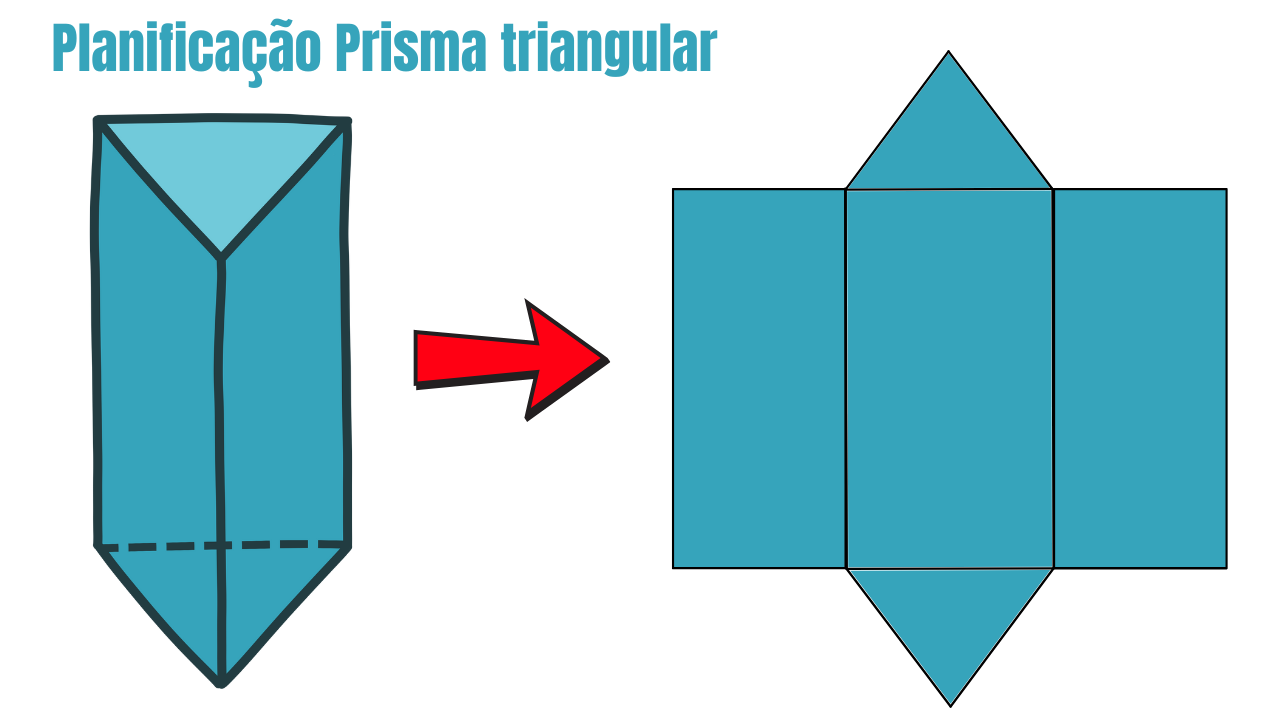
1) O que é a planificação (rede) do prisma triangular?
A planificação é o desenho plano que representa todas as faces do prisma “abertas” sobre o papel. Para o prisma triangular, a rede é composta por:
- 3 retângulos (faces laterais), todos com altura igual à altura do prisma \(h\) e larguras iguais aos três lados do triângulo da base;
- 2 triângulos congruentes (as bases), iguais ao triângulo da base do prisma.
Ao “colar” essa rede, recuperamos o sólido original.
2) Medidas e fórmulas na planificação
- Perímetro da base (soma dos três lados): \(p\).
- Faixa lateral (a soma dos três retângulos) tem dimensões \(p \times h\).
Aqui, \(A_b\) é a área do triângulo da base (veja fórmulas de área de triângulo).
3) Como construir a planificação (passo a passo)
- Calcule o perímetro do triângulo da base: \(p\).
- Desenhe um retângulo de dimensões \(p \times h\) (faixa lateral).
- Marque na largura \(p\) três segmentos consecutivos iguais aos lados da base, na mesma ordem dos lados do triângulo (isso separa os 3 retângulos laterais).
- Anexe dois triângulos (idênticos ao da base) em duas extremidades opostas da faixa (um em cima, outro em baixo, por exemplo).
- Recorte e dobre nas divisões: as faces laterais se unem e os triângulos fecham as bases.
Dica: mantenha a mesma ordem dos lados ao marcar os três retângulos, pois define quais arestas se encontram.
4) Dimensões dos retângulos por tipo de base
Base qualquer (escalena)
Lados \(a,b,c\). Retângulos: \(a\times h\), \(b\times h\), \(c\times h\).
Base retângula
Catetos \(b,c\) e hipotenusa \(\sqrt{b^2+c^2}\). Retângulos: \(b\times h\), \(c\times h\), \(\sqrt{b^2+c^2}\times h\).
Base equilátera
Lado \(a\). Retângulos: \(a\times h\), \(a\times h\), \(a\times h\).
Base isósceles
Lados \(a,a,b\). Retângulos: \(a\times h\), \(a\times h\), \(b\times h\).
5) Exemplos resolvidos (abre/fecha)
Exemplo 1 — Base equilátera (a=8 cm), h=10 cm
Peça: Liste as dimensões da rede e calcule \(A_L\) e \(A_T\).
$$\begin{aligned} p&=3a=3\cdot8=24\\ \text{Retângulos: }& 8\times10,\ 8\times10,\ 8\times10\\ A_L&=p\,h=24\cdot10= \boxed{240\ \text{cm}^2}\\ A_b&=\frac{\sqrt3}{4}a^2=\frac{\sqrt3}{4}\cdot64=16\sqrt3\\ A_T&=A_L+2A_b=240+2\cdot16\sqrt3=\boxed{240+32\sqrt3\ \text{cm}^2} \end{aligned}$$Exemplo 2 — Base retângula (6–8–10), h=12 cm
Peça: Descreva a rede e calcule \(A_L\), \(A_T\) e \(V\).
$$\begin{aligned} \text{Hipotenusa}&=\sqrt{6^2+8^2}=10\\ p&=6+8+10=24\\ \text{Retângulos: }& 6\times12,\ 8\times12,\ 10\times12\\ A_L&=p\,h=24\cdot12=\boxed{288\ \text{cm}^2}\\ A_b&=\frac{6\cdot8}{2}=24\\ A_T&=A_L+2A_b=288+48=\boxed{336\ \text{cm}^2}\\ V&=A_b\,h=24\cdot12=\boxed{288\ \text{cm}^3} \end{aligned}$$Exemplo 3 — Base escalena (7, 9, 12), h=15 cm
Peça: Dê as dimensões da rede e calcule \(A_L\) e \(A_T\).
$$\begin{aligned} p&=7+9+12=28\\ \text{Retângulos: }& 7\times15,\ 9\times15,\ 12\times15\\ s&=\frac{7+9+12}{2}=14\\ A_b&=\sqrt{14\cdot(14-7)\cdot(14-9)\cdot(14-12)}\\ &=\sqrt{14\cdot7\cdot5\cdot2}=\sqrt{980}=14\sqrt5\ \ (\approx 31{,}305)\\[2mm] A_L&=p\,h=28\cdot15=\boxed{420\ \text{cm}^2}\\ A_T&=A_L+2A_b=420+2\cdot14\sqrt5=\boxed{420+28\sqrt5\ \text{cm}^2}\ (\approx 482{,}35) \end{aligned}$$6) Erros comuns ao planificar
- Trocar a ordem dos lados na faixa lateral (isso altera que arestas se unem).
- Usar \(h\) errado: em prisma reto, \(h\) é a aresta lateral (distância entre as bases).
- Somar áreas de forma incorreta: lembre que \(A_T=A_L+2A_b\).
- Confundir área da base: escolha a fórmula certa (equilátero, retângulo/Heron, etc.).
7) Exercícios propostos (com soluções em formato vertical)
1) Base equilátera (a = 9 cm), altura do prisma h = 14 cm
Peça: Desenhe a planificação (dimensões) e calcule a área lateral e a área total.
Ver solução (vertical)
Planificação: três retângulos \(9\times14\), \(9\times14\), \(9\times14\) e duas bases triangulares equiláteras.
$$\begin{aligned} p &= 3a\\ &= 3\cdot 9\\ &= 27\\[4pt] A_L &= p\cdot h\\ &= 27\cdot 14\\ &= 378\ \text{cm}^2\\[8pt] A_b &= \frac{\sqrt3}{4}\,a^2\\ &= \frac{\sqrt3}{4}\cdot 9^2\\ &= \frac{\sqrt3}{4}\cdot 81\\ &= 20{,}25\sqrt3\ \text{cm}^2\\[8pt] A_T &= A_L + 2A_b\\ &= 378 + 2\cdot 20{,}25\sqrt3\\ &= 378 + 40{,}5\sqrt3\ \text{cm}^2 \end{aligned}$$2) Base retângula (catetos 8 cm e 15 cm), altura do prisma h = 10 cm
Peça: Liste os três retângulos da rede e calcule a área lateral e o volume.
Ver solução (vertical)
Planificação: retângulos \(8\times10\), \(15\times10\), \(17\times10\) (pois a hipotenusa é 17).
$$\begin{aligned} \text{hipotenusa} &= \sqrt{8^2 + 15^2}\\ &= \sqrt{64 + 225}\\ &= \sqrt{289}\\ &= 17\\[8pt] p &= 8 + 15 + 17\\ &= 40\\[4pt] A_L &= p\cdot h\\ &= 40\cdot 10\\ &= 400\ \text{cm}^2\\[8pt] A_b &= \frac{8\cdot 15}{2}\\ &= \frac{120}{2}\\ &= 60\ \text{cm}^2\\[8pt] V &= A_b\cdot h\\ &= 60\cdot 10\\ &= 600\ \text{cm}^3 \end{aligned}$$3) Base escalena (lados 5 cm, 7 cm, 10 cm), altura do prisma h = 18 cm
Peça: Calcule a área lateral, a área total e o volume (use Heron para a base).
Ver solução (vertical)
Aproximações: \(\sqrt{66}\approx 8{,}124\) → \(A_T\approx 396 + 32{,}496 = 428{,}496\ \text{cm}^2\); \(V\approx 36\cdot 8{,}124 = 292{,}5\ \text{cm}^3\).






















