Poliedros de Platão: o que são, exemplos e aplicações?

Neste guia direto ao ponto, você vai entender quem são os cinco poliedros regulares de Platão, por que eles são especiais, como aplicar a Relação de Euler $V-E+F=2$ e ver exemplos práticos com exercícios comentados (passo a passo, ideais para celular).

Introdução — por que estudar sólidos regulares e a relação de Euler?

Os Poliedros de Platão são os cinco sólidos convexos cujas faces são polígonos regulares congruentes e o mesmo número de faces se encontra em cada vértice. Aparecem em cristais, arte, design e ciência de materiais. Dominá-los facilita entender Geometria Espacial, reconhecer padrões de contagem (faces/arestas/vértices) e aplicar a Relação de Euler $V-E+F=2$ em problemas de provas e concursos. A seguir, você encontra definição, propriedades, imagens de cada sólido com características essenciais, exemplos práticos e uma lista final de exercícios com solução.

📘 Baixe grátis — eBook de Fórmulas de Matemática

Tenha as fórmulas-chave de Geometria (áreas, volumes e mais) sempre à mão.

Quero o eBook gratuito Ótimo para revisar áreas e volumes dos poliedros em 5 minutos.

Vídeo-aula — Poliedros de Platão e Relação de Euler

Dica: assista e, em seguida, resolva os exercícios ao final deste artigo.

Definição e propriedades essenciais dos sólidos regulares

Todas as faces são polígonos regulares congruentes.
O mesmo número de faces encontra-se em cada vértice.
São convexos e obedecem à Relação de Euler: $V-E+F=2$.
Existem exatamente cinco: tetraedro, cubo, octaedro, dodecaedro e icosaedro.

Leitura relacionada: Poliedros — guia completo · Sólidos de Platão — propriedades · Estrutura, Euler e Platão

Relação de Euler: como usar $V-E+F=2$ em problemas reais

Para poliedros convexos, vale: $V – E + F = 2$. Com ela, você descobre uma das contagens conhecendo as outras duas.

Exemplo prático (aplicação direta)

Enunciado: Um cubo possui $F=6$ e $V=8$. Calcule $E$.

Resolução:
$8 – E + 6 = 2 \Rightarrow$
$14 – E = 2 \Rightarrow$
$E = 12$.

Treine mais: Exercícios de Euler · Questão Cesgranrio comentada

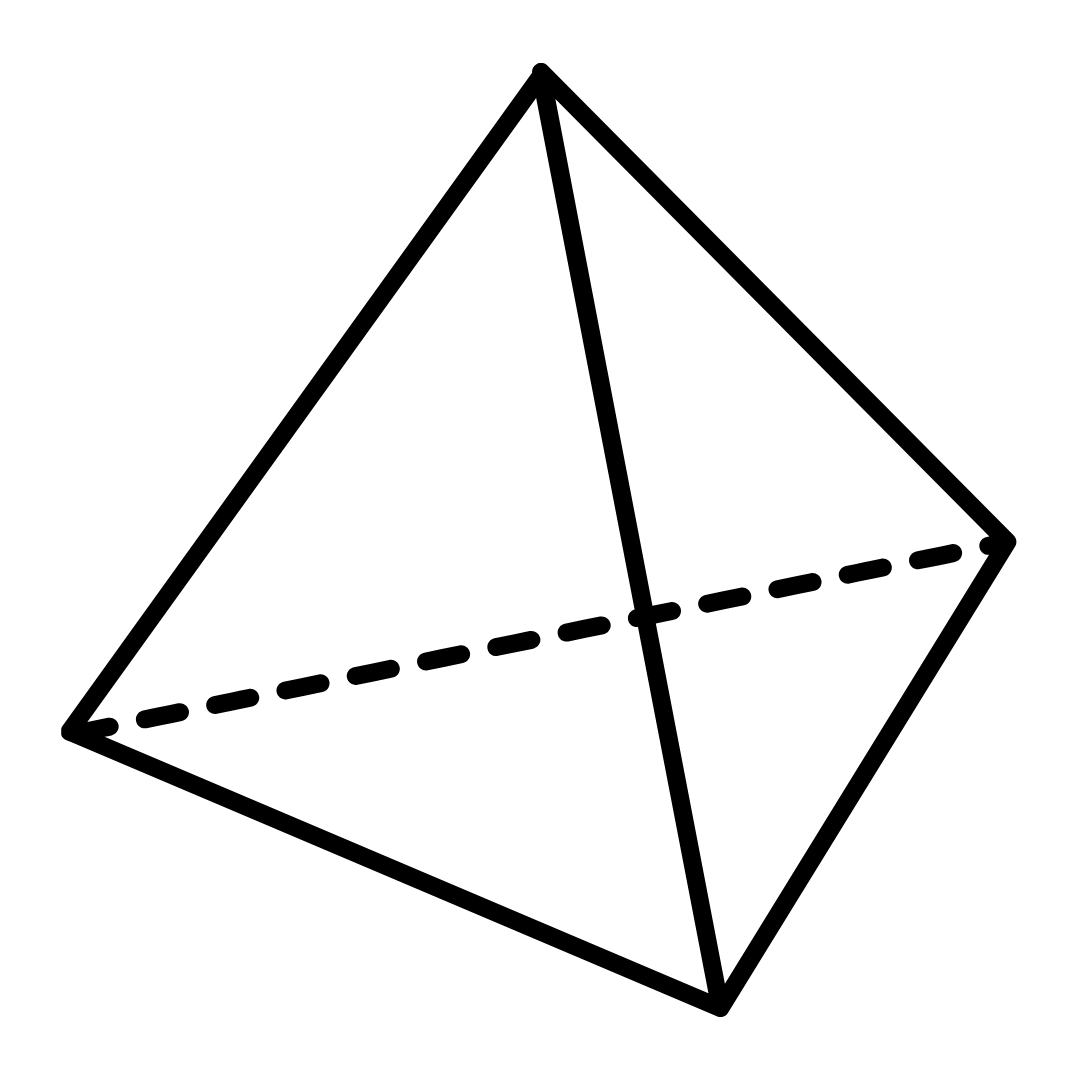
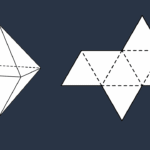
Tetraedro regular — características essenciais

Faces: 4
Formato das faces: triângulos equiláteros
Arestas: 6
Vértices: 4

Exemplo prático

Com aresta $a$, o volume é $V=\dfrac{a^3}{6\sqrt{2}}$. Para $a=3$ cm:
$V=\dfrac{27}{6\sqrt2}\Rightarrow\dfrac{9}{2\sqrt2}\,\text{cm}^3$.

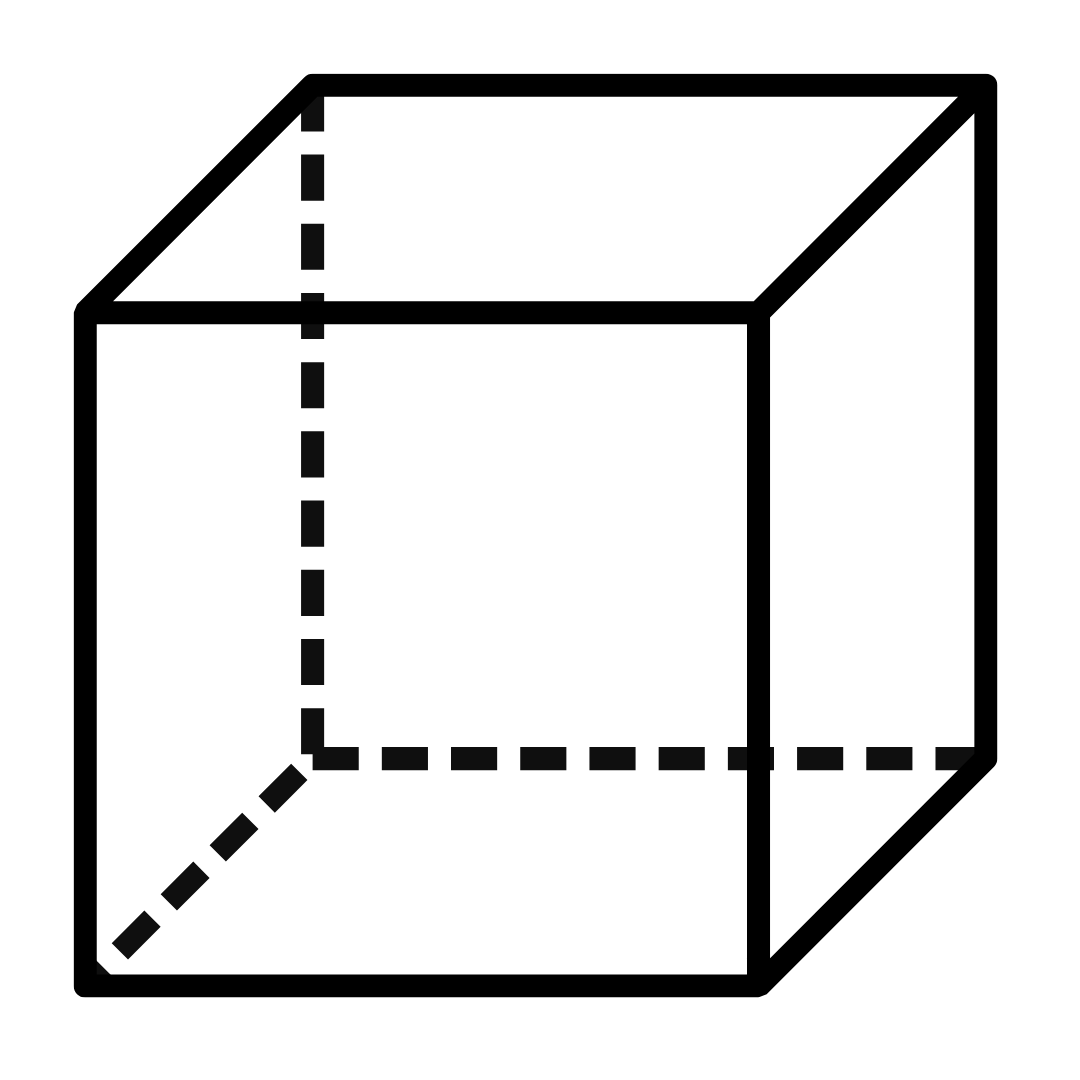
Cubo (Hexaedro) — características essenciais

Faces: 6
Formato das faces: quadrados
Arestas: 12
Vértices: 8

Exemplo prático

Com aresta $a$, $A_T=6a^2$ e $V=a^3$. Para $a=2$ cm:
$A_T=24\,\text{cm}^2$ e $V=8\,\text{cm}^3$.

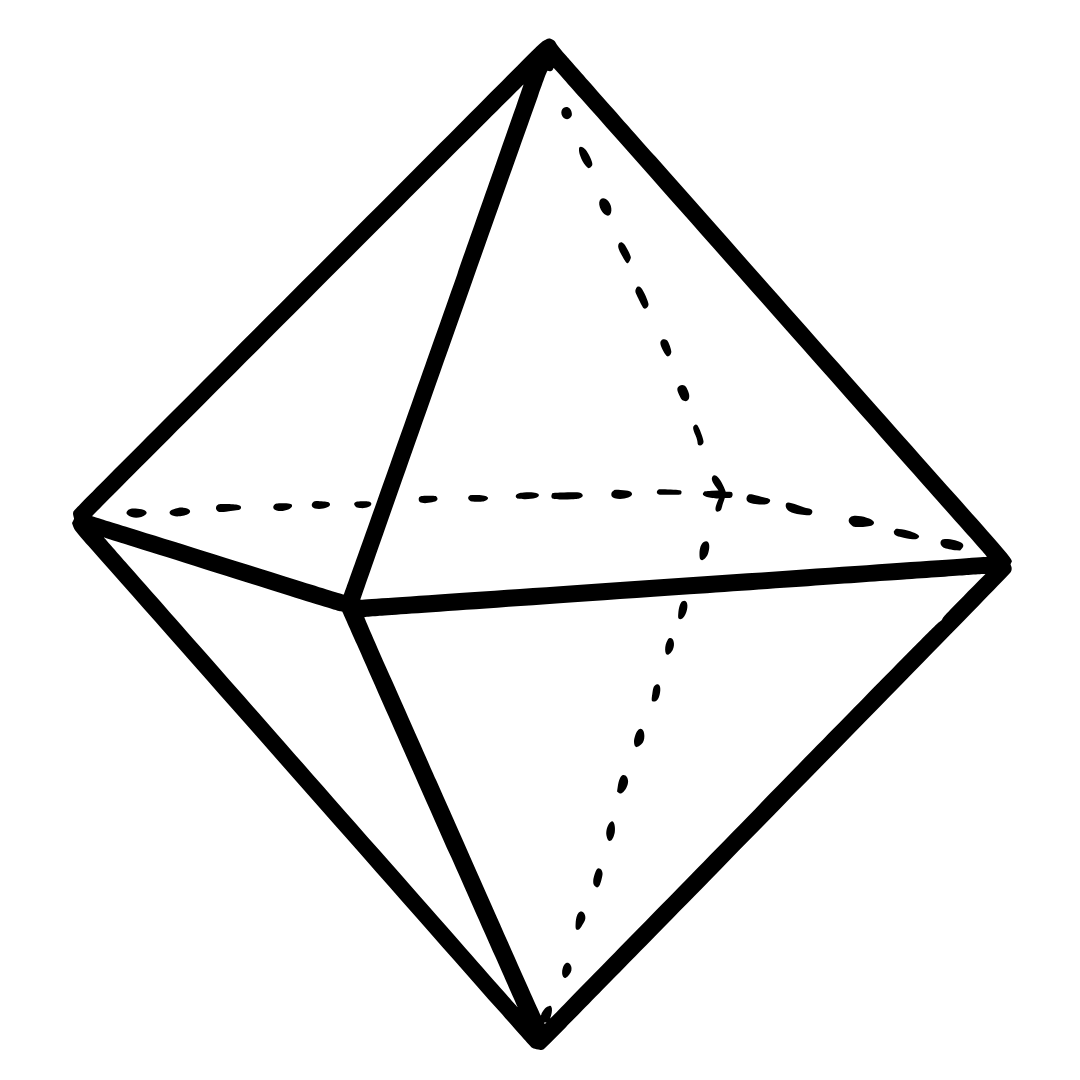
Octaedro — características essenciais

Faces: 8
Formato das faces: triângulos equiláteros
Arestas: 12
Vértices: 6

Verificação rápida

$V-E+F=6-12+8=2$ ✅

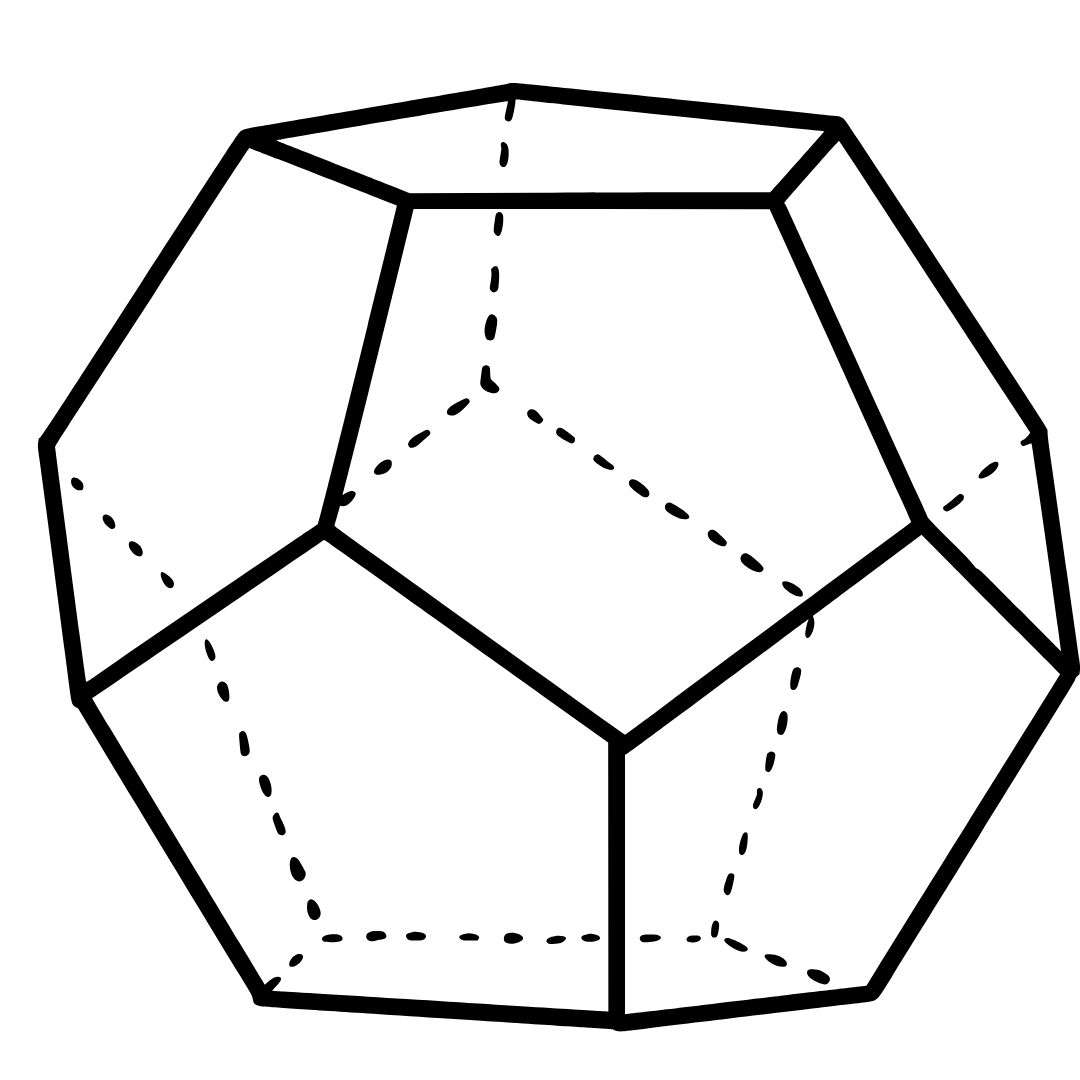
Dodecaedro — características essenciais

Faces: 12
Formato das faces: pentágonos regulares
Arestas: 30
Vértices: 20

Exemplo prático (Euler)

Com $F=12$ e $V=20$, então:
$20-E+12=2\Rightarrow E=30$.

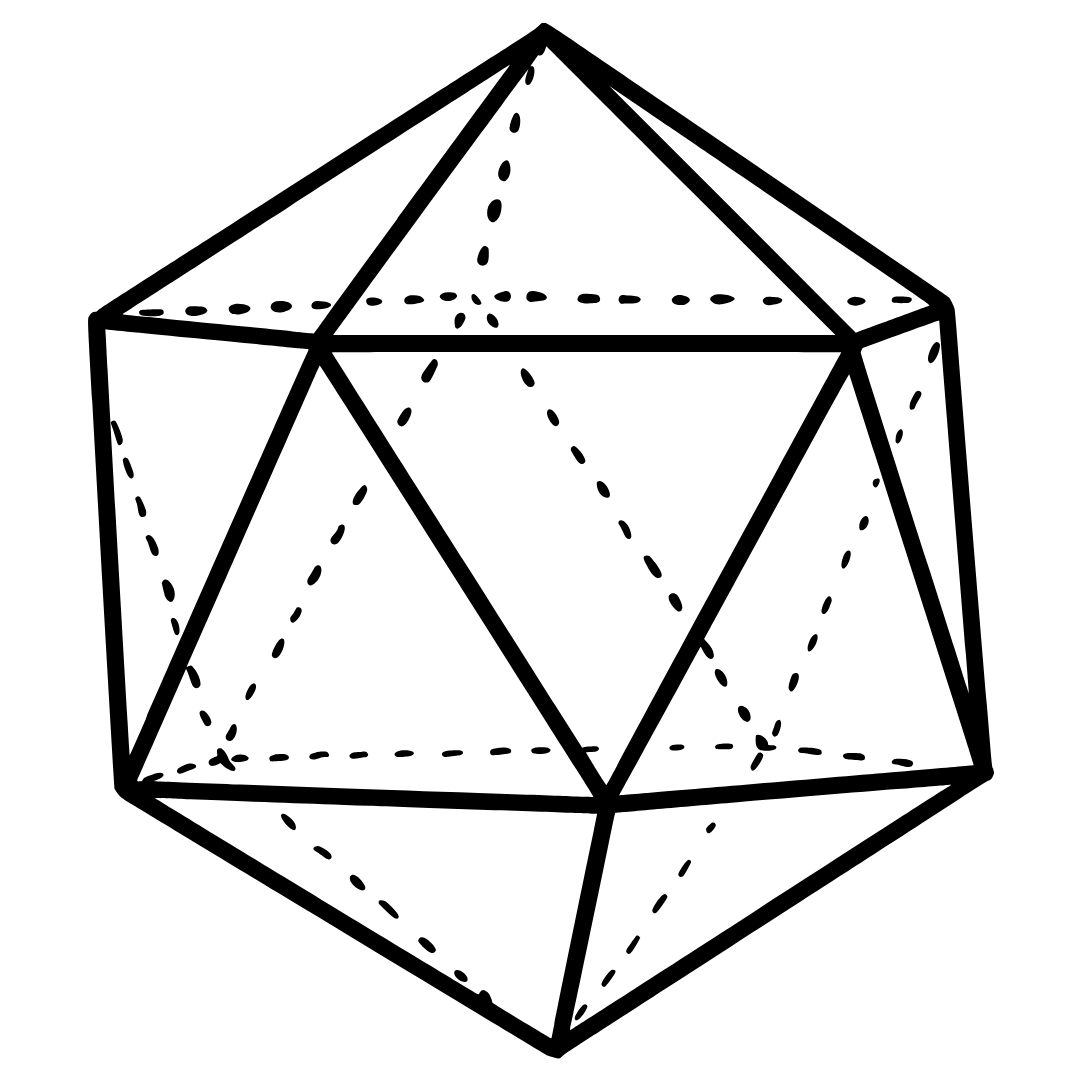
Icosaedro — características essenciais

Faces: 20
Formato das faces: triângulos equiláteros
Arestas: 30
Vértices: 12

Verificação rápida

$V-E+F=12-30+20=2$ ✅

🧠 Mapas Mentais de Matemática (visual e direto)

Fixe definições, Euler e fórmulas de áreas/volumes com esquemas práticos.

Acessar Mapas Mentais Inclui esquemas de poliedros, prismas e pirâmides.

Mais prática — prismas, pirâmides e família dos poliedros

Depois dos sólidos de Platão, avance para prismas e pirâmides com exercícios passo a passo.

Continue estudando: Poliedros e Corpos Redondos · Guia de Geometria Espacial · Lista de Exercícios — Poliedros

Recursos para estudar e praticar

Lista de exercícios — poliedros regulares e Euler

1) Contagem por Euler (nível básico)

Enunciado: Um poliedro convexo tem $V=10$ vértices e $F=8$ faces. Determine $E$.

👀 Mostrar/ocultar solução passo a passo

$V – E + F = 2 \Rightarrow$
$10 – E + 8 = 2 \Rightarrow$
$18 – E = 2 \Rightarrow$
$E = 16$.

2) Sólido de Platão (nível básico)

Enunciado: Em um dodecaedro regular, $F=12$ e $V=20$. Use Euler para achar $E$.

👀 Mostrar/ocultar solução passo a passo

$V – E + F = 2 \Rightarrow$
$20 – E + 12 = 2 \Rightarrow$
$32 – E = 2 \Rightarrow$
$E = 30$.

3) Questão estilo concurso (nível intermediário)

Enunciado: Um poliedro convexo tem $V=14$. Em 6 vértices concorrem 4 arestas, em 4 vértices concorrem 3 arestas e, nos demais, 5 arestas. Quantas faces o poliedro possui?

👀 Mostrar/ocultar solução passo a passo

Soma dos graus dos vértices é o dobro das arestas:
$6\cdot4 + 4\cdot3 + 4\cdot5 = 24 + 12 + 20 \Rightarrow$
$= 56 = 2E \Rightarrow$
$E = 28$.

Pela Relação de Euler:
$V – E + F = 2 \Rightarrow$
$14 – 28 + F = 2 \Rightarrow$
$F = 16$.

Veja a resolução detalhada no blog (Cesgranrio).

4) Verificação rápida (nível básico)

Enunciado: Verifique a Relação de Euler para o icosaedro: $F=20$, $E=30$, $V=12$.

👀 Mostrar/ocultar solução passo a passo

$V – E + F = 12 – 30 + 20 \Rightarrow$
$= 2$ ✅

📘 Reforço: baixe o eBook gratuito de Fórmulas

Use o resumo de áreas e volumes para revisar antes de exercícios e provas.

Baixar agora Conteúdo direto, visual e pronto para impressão.

Conclusão — leve isso para a prova e para a prática

Você viu quem são os cinco Poliedros de Platão, como aplicar a Relação de Euler para contar faces, arestas e vértices e praticou exercícios em formato “linha a linha”. Com esse repertório, fica mais fácil avançar para prismas e pirâmides. Volte quando precisar revisar!

Próximos passos: Fórmula de Euler — artigo · Sólidos de Platão — guia

FAQ — dúvidas rápidas sobre poliedros regulares

Quantos e quais são os Poliedros de Platão?

São cinco: tetraedro, cubo (hexaedro), octaedro, dodecaedro e icosaedro. Todos são convexos, regulares e obedecem à relação $V-E+F=2$. Cada um possui faces congruentes e o mesmo número de faces em cada vértice.

O que diz a Relação de Euler e quando usá-la?

Para poliedros convexos, $V – E + F = 2$. Ela permite calcular uma contagem (faces, arestas ou vértices) quando você conhece as outras duas. É ferramenta essencial em provas, concursos e exercícios de geometria espacial.

Como diferenciar poliedros de corpos redondos?

Poliedros têm apenas faces planas (polígonos), arestas e vértices. Corpos redondos possuem superfícies curvas, como cilindro, cone e esfera. Costuma-se estudar primeiro os poliedros e depois os redondos.

Quais links estudar depois dos sólidos regulares?

Recomendo os guias de prismas e pirâmides, listas de exercícios e o artigo completo da Relação de Euler. Use mapas mentais e o eBook gratuito para revisar áreas e volumes antes de simulados e provas.

Novidade