PRISMA REGULAR – Geometria Espacial
Volume, Área Lateral e Área Total (com exemplos e exercícios)
O que é um prisma regular?
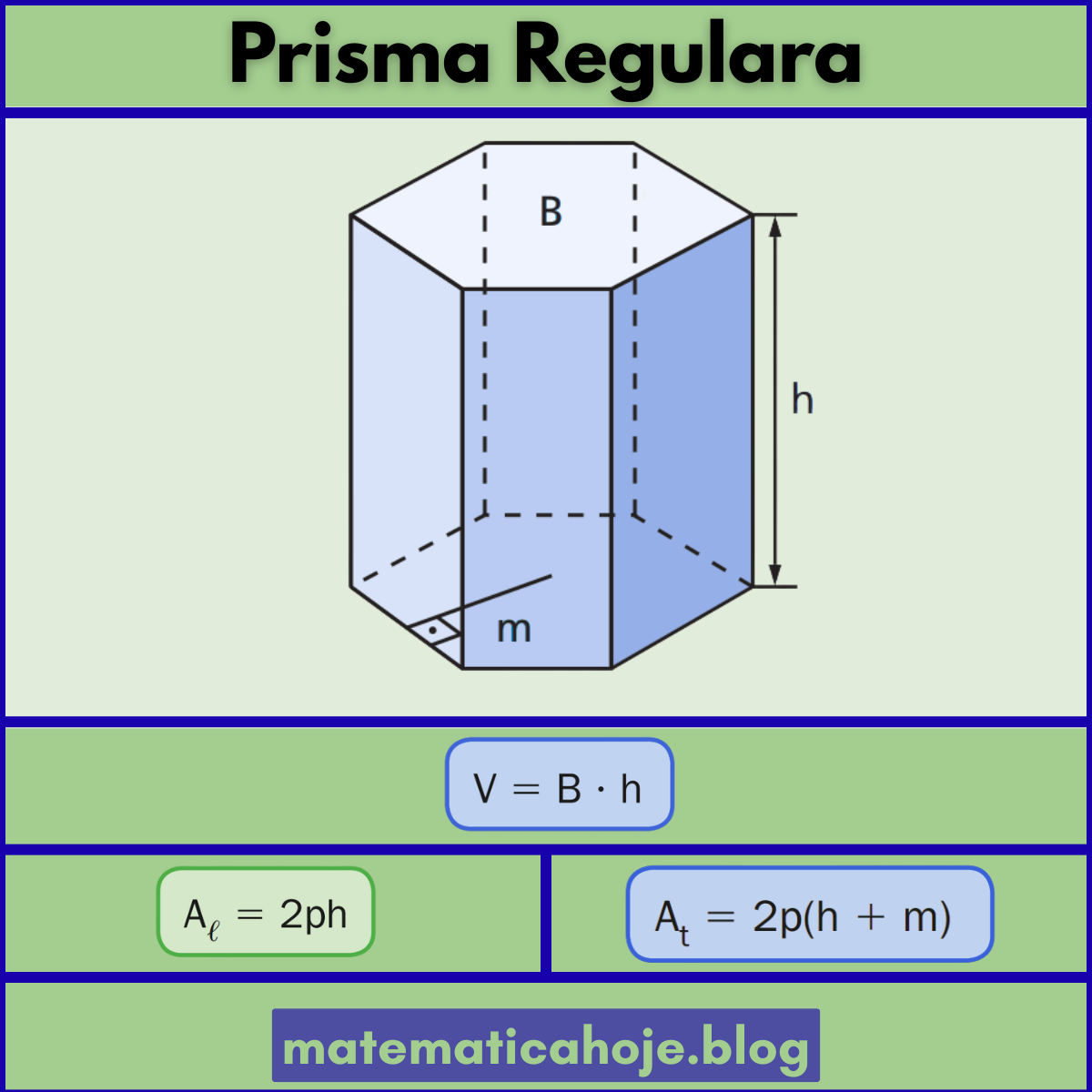
Chamamos de prisma regular reto o prisma cuja base é um polígono regular (todos os lados e ângulos iguais) e cujas arestas laterais são perpendiculares ao plano da base. Denotaremos por \(p\) o perímetro da base, por \(m\) o apótema da base, por \(B\) a área da base e por \(h\) a altura do prisma.
🧠 Mapas Mentais de Matemática
📘 Banco de Questões
🎯 Guia do ENEM
📚 Coleção completa
📘 Fórmulas do Prisma Regular Reto
Com \(p\) (perímetro da base), \(m\) (apótema da base), \(B\) (área da base) e \(h\) (altura):
Exemplo 1 (hexágono regular)
Considere um prisma regular reto de base hexagonal com lado \(a=4\,\text{cm}\) e altura \(h=10\,\text{cm}\). Para o hexágono regular: \(p=6a\) e \(m=\dfrac{\sqrt{3}}{2}a\). Calcule \(V\), \(A_\ell\) e \(A_t\).
📗 Baixe o eBook de Fórmulas Matemáticas
Todas as fórmulas (Álgebra, Geometria Espacial, Trigonometria…) em um único PDF para consulta rápida.
📥 Baixar AgoraExemplos Adicionais
Exemplo 2 (pentágono regular). Em um prisma regular de base pentagonal, \(p=30\,\text{cm}\), \(m=4\,\text{cm}\) e \(h=12\,\text{cm}\). Calcule \(B\), \(V\), \(A_\ell\) e \(A_t\).
Exercícios de Múltipla Escolha
1. (Volume) Um prisma regular reto tem base triangular equilátera de lado \(a=6\,\text{cm}\) e altura do prisma \(h=8\,\text{cm}\). Calcule o volume.
Dado: área do triângulo equilátero \(B=\dfrac{a^2\sqrt{3}}{4}\).
👀 Ver solução passo a passo
Gabarito: B.
2. (Área total) Em um prisma regular de base pentagonal, \(p=40\,\text{cm}\), \(m=5\,\text{cm}\) e \(h=12\,\text{cm}\). Determine a área total.
👀 Ver solução passo a passo
Gabarito: C.
3. (Altura) Um prisma regular de base hexagonal tem \(p=36\,\text{cm}\), \(m=3\,\text{cm}\) e volume \(V=972\,\text{cm}^3\). Encontre a altura \(h\).
👀 Ver solução passo a passo
Gabarito: C.
Conclusão
As relações \(V=B\cdot h\), \(A_\ell=p\cdot h\) e \(A_t=2B+p h=p(h+m)\) resolvem praticamente todos os problemas de prismas regulares retos em provas e no ENEM. Continue estudando com: