Probabilidade – Matemática CESPE – Concurso Público

(CESPE / CEBRASPE  2024 – Prefeitura de Camaçari – BA – Professor Matemática)

Uma urna contém 12 bolas azuis e 12 bolas vermelhas. Se duas bolas são retiradas aleatoriamente da urna, uma em sequência da outra e sem reposição, a probabilidade de se tirar duas bolas de cores diferentes é igual a

A) 6/23

B) 11/23

C) 12/23

D) 1/4

E) 1/2

Solução em vídeo

Para resolver esse problema, vamos calcular a probabilidade de retirar duas bolas de cores diferentes (uma azul e uma vermelha) em sequência e sem reposição.

Passo 1: Total de bolas

• A urna contém 12 bolas azuis e 12 bolas vermelhas, totalizando:
  12 + 12 = 24 bolas

Passo 2: Probabilidade de tirar duas bolas de cores diferentes

Existem duas possibilidades para que as bolas retiradas sejam de cores diferentes:

1. A primeira bola é azul e a segunda é vermelha.
2. A primeira bola é vermelha e a segunda é azul.

Vamos calcular a probabilidade de cada caso.

Caso 1: A primeira bola é azul e a segunda é vermelha

• A probabilidade de retirar uma bola azul na primeira retirada é:

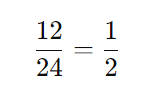
• Depois de retirar uma bola azul, restam 23 bolas na urna, sendo 12 vermelhas. A probabilidade de retirar uma bola vermelha na segunda retirada é:
  
  12/23
  
• Portanto, a probabilidade de retirar primeiro uma bola azul e depois uma vermelha é:

Caso 2: A primeira bola é vermelha e a segunda é azul

• A probabilidade de retirar uma bola vermelha na primeira retirada é:

• Depois de retirar uma bola vermelha, restam 23 bolas na urna, sendo 12 azuis. A probabilidade de retirar uma bola azul na segunda retirada é:

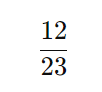
• Portanto, a probabilidade de retirar primeiro uma bola vermelha e depois uma azul é:

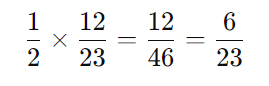
Passo 3: Somar as probabilidades dos dois casos

Como os dois casos são mutuamente exclusivos (ou ocorre um ou o outro), somamos as probabilidades:

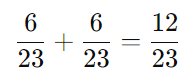
Resposta:

A probabilidade de retirar duas bolas de cores diferentes é 12/23, portanto, a resposta correta é a alternativa:

C) 12/23.