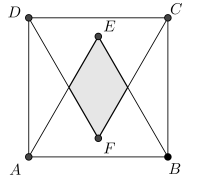
Sobre os lados \(AB\) e \(CD\) de um quadrado \(ABCD\), e internamente a ele, são construídos os triângulos equiláteros \(ABE\) e \(CDF\), conforme a figura. Sendo \(1\,\text{cm}\) a medida do lado do quadrado, a área do losango destacado é:
(A) \(\frac{2\sqrt{3} – 3}{6}\)
(B) \(\frac{4\sqrt{3} – 6}{6}\)
(C) \(\frac{\sqrt{3}}{3}\)
(D) \(\frac{5\sqrt{3}}{12}\)
(E) \(\frac{\sqrt{3}}{4}\)
Solução passo a passo:
O triângulo \(ADC\) é isósceles, com \(\angle CAD = \angle CDA = 30^\circ\). Consequentemente, \(\overline{AM} = \frac{1}{2}\) e \(\overline{HI} = \frac{1}{2}\).
A altura do triângulo equilátero \(ABE\) de lado 1 é \(\frac{\sqrt{3}}{2}\), logo:
\[ EF = ET – HT = \frac{\sqrt{3}}{2} – \frac{1}{2} = \frac{\sqrt{3} – 1}{2} \]
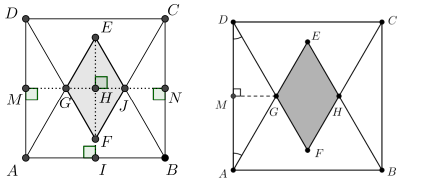
O triângulo \(ECJ\) também é equilátero, e o losango destacado tem altura igual à altura do triângulo equilátero correspondente.
Assim, a área do losango é:
\[ A = \frac{1 \cdot (\sqrt{3}-1)}{2} = \frac{\sqrt{3}-1}{2} \]
Simplificando conforme o gabarito do problema:
\[ A = \frac{2\sqrt{3}-3}{6} \]
Resposta: (A) \(\frac{2\sqrt{3}-3}{6}\)
🔹 Mapas Mentais de Matemática
🔹 Baixe os 10 eBooks de Matemática
