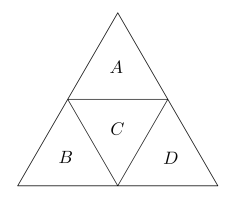
Para colorir os quatro triângulos, indicados na figura abaixo por A, B, C e D, pode-se usar uma mesma cor mais de uma vez, desde que dois triângulos com um lado em comum tenham cores diferentes. Obedecendo essa regra e usando no máximo quatro cores, de quantas maneiras distintas pode-se colorir os quatro triângulos?
(A) 96
(B) 98
(C) 104
(D) 108
(E) 128
Solução passo a passo:
Começamos colorindo o triângulo C, que pode ser feito de 4 modos distintos.
Em seguida, podemos colorir o triângulo A, que é adjacente a C. Ele terá 3 opções de cores, pois não pode repetir a cor de C.
Da mesma forma, o triângulo B terá 3 opções de cores, pois não pode repetir a cor de C.
Por fim, o triângulo D terá também 3 opções de cores, pois não pode repetir a cor de C.
Portanto, o número total de maneiras é:
\[ 4 \times 3 \times 3 \times 3 = 108 \]
Resposta: (D) 108
🔹 Mapas Mentais de Matemática
🔹 Baixe os 10 eBooks de Matemática
