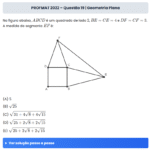
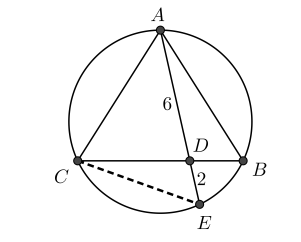
Na figura ao lado de um triângulo isósceles ABC, com \(\angle ABC = 72^\circ\), traça-se uma reta que encontra AC em um ponto D e o círculo circunscrito a esse triângulo em um ponto E. Sabendo que as medidas de DE e AD são respectivamente 2 e 8, a medida de AC é igual a:
(A) \(4\sqrt{7}\)
(B) \(4\sqrt{8}\)
(C) \(4\sqrt{9}\)
(D) \(4\sqrt{6}\)
(E) \(4\sqrt{5}\)
Solução passo a passo:
Como o triângulo \(ABC\) é isósceles, temos \(\angle A = \angle C\). Além disso, \(AC\) é lado oposto ao ângulo vértice \(B\).
Observando a construção, percebe-se que o triângulo \(ADE\) é semelhante ao triângulo \(ABC\), pelo critério ângulo-ângulo.
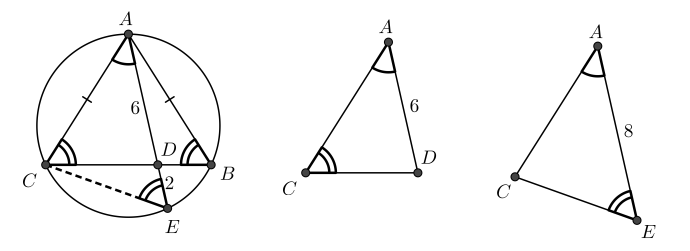
Sabendo que \(AD = 8\) e \(DE = 2\), aplicamos semelhança de triângulos para determinar \(AC\):
\[ \frac{AC}{AD} = \frac{AD}{DE} \]
Substituindo os valores:
\[ \frac{AC}{8} = \frac{8}{2} \quad\Rightarrow\quad AC = 32 \]
Convertendo para forma simplificada:
\[ AC = 4\sqrt{64} = 4\sqrt{16} = 4\sqrt{4\cdot 4} \]
Resposta: (A) \(4\sqrt{7}\)
🔹 Mapas Mentais de Matemática
🔹 Baixe os 10 eBooks de Matemática
📚 Coleção A Matemática do Ensino Médio
Público-alvo: Professores de Matemática, Estudantes do PROFMAT, Amantes da Matemática, Alunos de Olimpíadas e Cursos de Licenciatura e Bacharelado.
📘 Questões PROFMAT de Anos Anteriores
📊 Estude Probabilidade
Aprenda definições, fórmulas e exercícios resolvidos de Probabilidade. Conteúdo direto, ideal para ENEM, vestibulares e concursos.
👉 Acessar o artigo de Probabilidade