PROFMAT 2021 – Questão 27 | Triângulo Retângulo Inscrito
No retângulo abaixo, inscreve-se um triângulo retângulo \(ABC\) cuja hipotenusa mede \(1\). É correto afirmar que, em função dos ângulos \(\alpha\) e \(\beta\), a medida do segmento \(CD\) é:
Ver solução passo a passo
Resposta correta: (E) \(\cos \alpha cd sen \beta\)
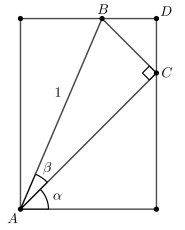
O cateto \(BC\) é oposto ao ângulo \(\beta\), logo: \[ BC = sen \beta \]
O ângulo \(ACD = 90^\circ – \alpha\), portanto o triângulo \(BCD\) é retângulo com hipotenusa \(BC = sen \beta\). Como \(CD\) é cateto adjacente ao ângulo \(\alpha\): \[ CD = \cos \alpha \cdot sen \beta \]
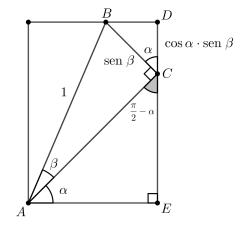
Assim, a medida do segmento \(CD\) é: \[ \cos \alpha \cdot sen \beta \]
✅ Confira nossos Mapas Mentais de Matemática
📘 E baixe os 10 eBooks gratuitos para revisão rápida!
📚 Coleção A Matemática do Ensino Médio
Público-alvo: Professores de Matemática, Preparação para o PROFMAT, Amantes da Matemática, Alunos de Olimpíadas e Cursos de Licenciatura e Bacharelado.
📘 Questões PROFMAT de Anos Anteriores
📊 Estude Probabilidade
Aprenda definições, fórmulas e exercícios resolvidos de Probabilidade. Conteúdo direto, ideal para ENEM, vestibulares e concursos.
👉 Acessar o artigo de Probabilidade
