Dois postes verticais têm 8 metros e 10 metros de altura, respectivamente, e suas bases, apoiadas em um chão perfeitamente plano e horizontal, distam 20 metros entre si. Se um ponto do segmento que une as bases dos postes está à mesma distância dos topos dos postes, a distância em metros deste ponto à base do poste mais baixo é:
(B) 10
(C) \(10 – 2\sqrt{5}\)
(D) \(10 + 2\sqrt{5}\)
(E) 11
Resposta correta: (A) 10,9
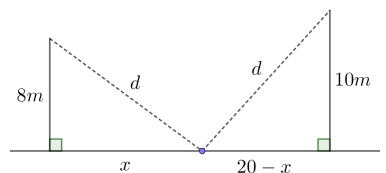
Seja \(x\) a distância do ponto à base do poste de 8 m. Então a distância ao poste de 10 m será \(20-x\). Aplicando o Teorema de Pitágoras:
\[ d^2 = 8^2 + x^2 \] \[ d^2 = 10^2 + (20-x)^2 \]
Igualando: \[ 64 + x^2 = 100 + (20-x)^2 \] \[ 64 + x^2 = 100 + 400 – 40x + x^2 \] \[ 40x = 436 \Rightarrow x = 10,9 \]
🔗 Continue seus estudos:





























