PROFMAT 2024 – Questão 27 | Geometria Plana e Área de Quadrados
\(ABCD\) é um quadrado de lado 4. Tomam-se os pontos \(E\) e \(G\) sobre os lados \(AD\) e \(BC\), tais que \(DE = BG = 1\) e constrói-se o quadrado \(EHIG\), conforme a figura:
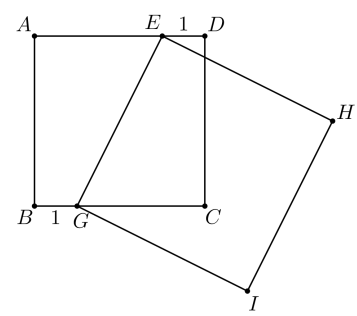
A área do quadrado \(EHIG\) é igual a:
(A) \( 4\sqrt{2} \)
(B) \( 2\sqrt{5} \)
(C) 20
(D) \( 5\sqrt{3} \)
(E) 17
(B) \( 2\sqrt{5} \)
(C) 20
(D) \( 5\sqrt{3} \)
(E) 17
Resposta correta: (C) 20.
Seja \( L \) o lado do quadrado \(EHIG\). Traçando-se a paralela de \(E\) ao lado \(CD\) até encontrar \(BC\) em \(P\), o triângulo \(EPG\) é retângulo com catetos: \[ 4 \quad \text{e} \quad 2 \]
Aplicando o Teorema de Pitágoras: \[ L^2 = 4^2 + 2^2 = 16 + 4 = 20 \] Logo, a área do quadrado é: \[ L^2 = 20 \]
🔗 Continue seus estudos com nossos recursos: