Proporcionalidade direta e função linear
Quando duas grandezas variam mantendo a mesma razão, existe proporcionalidade direta. Algebricamente: \(y=ax\), que é exatamente a função linear. Para revisar gráficos, taxa e sinais, confira a sequência abaixo:
Definição e propriedades essenciais
- Razão constante: \( \dfrac{y}{x}=a \) (com \(x\neq 0\)).
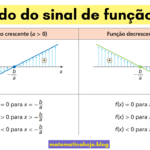
- Inclinação: \(a\) é o coeficiente angular (sobe se \(a>0\), desce se \(a<0\)).
- Gráfico: reta que passa pela origem \((0,0)\).
- Unidades: \(a\) tem unidade \([\text{y}]/[\text{x}]\) (km/h, R$/unidade, etc.).
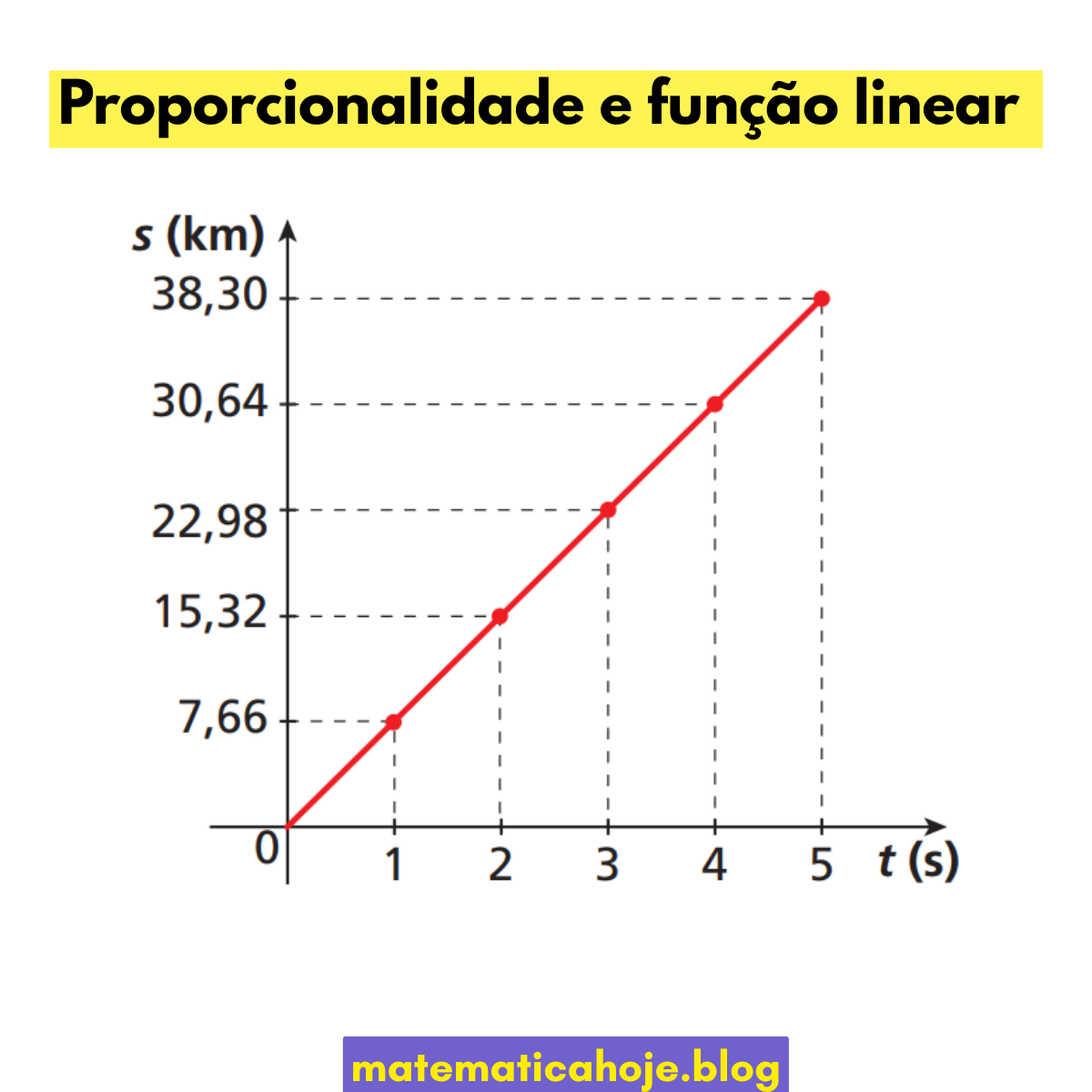
Como identificar em uma tabela
| \(x\) | \(y\) | \(y/x\) |
|---|---|---|
| 1 | 7,66 | 7,66 |
| 2 | 15,32 | 7,66 |
| 3 | 22,98 | 7,66 |
| 4 | 30,64 | 7,66 |
Como \(y/x\) é constante, \(y=7{,}66\,x\). É o mesmo raciocínio da regra de três direta.
Do enunciado para a lei \(y=ax\) (regra de três ↔ função)
- Leia o par conhecido (ex.: “em 2 h, percorre 15,32 km” ⇒ \(x=2\), \(y=15{,}32\)).
- Calcule \(a=\dfrac{y}{x}\).
- Escreva \(y=ax\) e use para prever qualquer valor.
Se houver termo independente \(b\neq 0\), não é proporcionalidade direta; trata-se de função afim \(y=ax+b\). Para sinais/zeros: estudo do sinal e zero.
Interpretação geométrica e taxa
É a subida/avanço entre dois pontos da reta. Relembre a interpretação completa em Δy/Δx.
📘 Precisa das fórmulas na mão?
Baixe o eBook Fórmulas Matemática com resumos de funções, gráficos, geometria e estatística. Perfeito para revisão rápida antes das provas.
Baixar eBook de FórmulasExemplos resolvidos
Exemplo 1 — Movimento uniforme (modelagem completa).
Um ciclista se desloca em pista plana com velocidade constante. Sabe-se que em \(2\,\text{h}\) ele percorre \(30{,}64\,\text{km}\).
Pede-se: a) escrever a função distância \(s(t)\) (em km) em função do tempo \(t\) (em horas); b) calcular \(s(5)\);
c) determinar o tempo necessário para atingir \(38{,}30\,\text{km}\). Apresente os resultados com duas casas decimais.
Ver solução
a) Proporcionalidade direta \(s(t)=vt\). \(v=30{,}64/2=15{,}32\). Logo \(s(t)=15{,}32\,t\).
b) \(s(5)=15{,}32\cdot5=76{,}60\ \text{km}\).
c) Resolver \(15{,}32\,t=38{,}30\Rightarrow t\approx2{,}50\ \text{h}\).
Exemplo 2 — Escala cartográfica (unidades e conversão).
Em um mapa na escala \(1:50\,000\), cada \(1\ \text{cm}\) representa a mesma distância real.
Sabendo que \(1\ \text{cm}\) equivale a \(0{,}5\ \text{km}\), determine: a) a função distância real \(D(c)\) (em km) em função dos centímetros \(c\) no mapa;
b) a distância real correspondente a \(7{,}2\ \text{cm}\) no mapa. Arredonde às centésimas.
Ver solução
a) Proporcionalidade direta: \(D(c)=0{,}5\,c\).
b) \(D(7{,}2)=0{,}5\cdot7{,}2=3{,}60\ \text{km}\).
Exemplo 3 — Custo variável puro (sem taxa fixa).
Uma gráfica cobra R$ 0,80 por página impressa, sem cobrança mínima.
a) Modele o custo \(C(p)\) (em reais) em função do número de páginas \(p\).
b) Calcule o valor de \(C(125)\).
c) Quantas páginas podem ser impressas com R$ 250,00? Considere valores exatos.
Ver solução
a) \(C(p)=0{,}80\,p\).
b) \(C(125)=0{,}80\cdot125=R\$100{,}00\).
c) Resolver \(0{,}80\,p=250 \Rightarrow p=312{,}5\). Como páginas são inteiras, no máximo \(312\) páginas (R$249,60) e sobra R$0,40.
Erros comuns
- Confundir proporcionalidade direta com função afim quando há taxa fixa \(b\neq 0\).
- Comparar \(y/x\) com arredondamentos diferentes; padronize as casas decimais.
- Esquecer unidades na constante \(a\).
Exercícios propostos (enunciados mais completos)
1) Densidade de material. A massa \(m\) (em g) é diretamente proporcional ao volume \(V\) (em cm³). Sabe-se que uma amostra tem \(m=12\,\text{g}\) quando \(V=4\,\text{cm}^3\). a) Determine a constante de proporcionalidade \(k\) (inclua as unidades). b) Escreva a função \(m(V)\). c) Calcule a massa para \(V=15\,\text{cm}^3\).
Ver gabarito
a) \(k=12/4=3\ \text{g/cm}^3\). b) \(m(V)=3V\). c) \(m(15)=45\ \text{g}\).
2) Tempo de produção. O tempo \(T\) (em minutos) é diretamente proporcional à quantidade \(q\) (peças). Em um teste, \(T=18\) quando \(q=12\). a) Encontre a constante \(a\) e escreva \(T(q)\). b) Estime o tempo para \(45\) peças. c) Quantas peças podem ser produzidas em \(2\) horas?
Ver gabarito
a) \(a=18/12=1{,}5\,\text{min/un}\) ⇒ \(T(q)=1{,}5\,q\).
b) \(T(45)=67{,}5\ \text{min}\).
c) \(2\ \text{h}=120\ \text{min}\). Resolver \(1{,}5\,q=120\Rightarrow q=80\) peças.
3) Validação de proporcionalidade. Dadas as medições \((2,7)\), \((5,18)\), \((8,29)\) (na ordem \(x,y\)), a) verifique se há proporcionalidade direta comparando as razões \(y/x\); b) se não houver, indique se um modelo afim \(y=ax+b\) poderia ser mais adequado (sem calcular \(a\) e \(b\)).
Ver gabarito
a) Razões: \(3{,}5\), \(3{,}6\), \(3{,}625\) (não iguais) ⇒ não é proporcionalidade direta.
b) Como as diferenças são quase constantes, um modelo afim pode ajustar melhor.
4) Ritmo de corrida. Um atleta mantém ritmo constante de 4 min por km. a) Modele a distância \(d(t)\) (em km) em função do tempo \(t\) (em minutos). b) Quanto ele percorre em 50 min? c) Quanto tempo para completar 21 km (meia-maratona)?
Ver gabarito
a) \(v=1/4=0{,}25\ \text{km/min}\) ⇒ \(d(t)=0{,}25\,t\).
b) \(d(50)=12{,}5\ \text{km}\).
c) Resolver \(0{,}25\,t=21\Rightarrow t=84\ \text{min}\) (1h24min).
5) Farmacologia básica. A concentração \(C\) (mg/L) é diretamente proporcional à dose \(D\) (mg). Para \(D=80\) mg, obtém-se \(C=2\) mg/L. a) Escreva \(C(D)\) e informe a constante com unidades. b) Determine a dose para obter \(C=3{,}5\) mg/L. c) Se a dose máxima segura é \(160\) mg, qual a concentração máxima obtida pelo modelo?
Ver gabarito
a) \(a=2/80=0{,}025\ \text{(mg/L)}/\text{mg}\) ⇒ \(C(D)=0{,}025\,D\).
b) \(D=3{,}5/0{,}025=140\ \text{mg}\).
c) \(C(160)=0{,}025\cdot160=4{,}0\ \text{mg/L}\).
Continue estudando
- Função linear • Função constante
- Como construir o gráfico da função afim
- Taxa de variação da função afim
- Zero da função afim • Interseção de retas
- Estudo do sinal da função afim